the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Error propagation in spectrometric functions of soil organic carbon
Monja Ellinger
Ines Merbach
Ulrike Werban
Soil organic carbon (SOC) plays a major role concerning chemical, physical, and biological soil properties and functions. To get a better understanding of how soil management affects the SOC content, the precise monitoring of SOC on long-term field experiments (LTFEs) is needed. Visible and near-infrared (Vis–NIR) reflectance spectrometry provides an inexpensive and fast opportunity to complement conventional SOC analysis and has often been used to predict SOC. For this study, 100 soil samples were collected at an LTFE in central Germany by two different sampling designs. SOC values ranged between 1.5 % and 2.9 %. Regression models were built using partial least square regression (PLSR). In order to build robust models, a nested repeated 5-fold group cross-validation (CV) approach was used, which comprised model tuning and evaluation. Various aspects that influence the obtained error measure were analysed and discussed. Four pre-processing methods were compared in order to extract information regarding SOC from the spectra. Finally, the best model performance which did not consider error propagation corresponded to a mean RMSEMV of 0.12 % SOC (R2=0.86). This model performance was impaired by ΔRMSEMV=0.04 % SOC while considering input data uncertainties (ΔR2=0.09), and by ΔRMSEMV=0.12 % SOC (ΔR2=0.17) considering an inappropriate pre-processing. The effect of the sampling design amounted to a ΔRMSEMV of 0.02 % SOC (ΔR2=0.05). Overall, we emphasize the necessity of transparent and precise documentation of the measurement protocol, the model building, and validation procedure in order to assess model performance in a comprehensive way and allow for a comparison between publications. The consideration of uncertainty propagation is essential when applying Vis–NIR spectrometry for soil monitoring.
- Article
(3161 KB) - Full-text XML
- BibTeX
- EndNote
Soil is at the same time one of the most important and one of the most limited natural resources. Most of all, it is needed for food production, as well as for the production of energy crops and fibre, and for the provision of freshwater (Johnson, 2008; Lorenz and Lal, 2016). All these aspects depend on the quality of the soil, which is determined by its site-specific properties. And this quality, in turn, is much influenced by its soil organic carbon (SOC) content since it affects chemical, physical, and biological soil properties and functions (Knadel et al., 2015; Lorenz and Lal, 2016). Additionally, SOC is also relevant in the context of global warming since the soil is the largest terrestrial reservoir of organic carbon (Conforti et al., 2015; Johnson, 2008; McBratney et al., 2014; Stockmann et al., 2011). SOC sequestration may lead to long-term SOC storage in relatively stable soil fractions (Lal, 2004; McBratney et al., 2014). Thus, the SOC stocks of soils could be used as a manageable sink for atmospheric carbon (Stockmann et al., 2011), achieving both food security and a strategy against the increasing CO2 concentration in the atmosphere (Lal, 2004; Lorenz and Lal, 2016; McBratney et al., 2014). As the SOC content of soils reacts very slowly to environmental changes (Meersmans et al., 2009), long-term field experiments (LTFEs) are required to understand the impact of soil management and farming systems on the rate of SOC sequestration (Lal, 2004), as well as on yield and crop quality in the long run.
The precise monitoring of SOC on an LTFE with conventional laboratory analysis is labour- and cost-intensive (Adamchuk and Viscarra Rossel, 2010; Loum et al., 2016) as it requires the analysis of a rather high number of samples. Visible and near-infrared (Vis–NIR) reflectance spectrometry can facilitate this procedure. It is non-destructive, fast, and economical (Mouazen et al., 2010) and requires the conventional laboratory analysis to be conducted on only a small number of soil samples, as well as little sample preparation (Conforti et al., 2015). The obtained spectrum contains information about many different soil components (Conforti et al., 2015; Viscarra Rossel et al., 2006b); please compare Stenberg et al. (2010) for a review on the past and current role of Vis–NIR spectrometry in soil science. Spectral absorption features are caused by vibrational stretching and bending of structural molecule groups and electronic excitation (Ben-Dor et al., 1999; Dalal and Henry, 1986). Molecule vibrations from hydroxyl, carboxyl, and amine functional groups produce absorption features related to soil organic matter in the mid-infrared (MIR) region of the spectra (Croft et al., 2012). In comparison, Vis–NIR spectra show only broad and unclear adsorption features related to overtone vibrations from the MIR, but instruments are less cost-intensive and available for field monitoring as well (Stenberg and Viscarra Rossel, 2010; Viscarra Rossel et al., 2006a). Furthermore, in diffuse reflectance spectroscopy, scattering properties depend on the particular wavelengths and can vary significantly over the Vis–NIR spectral range (Pilorget et al., 2016). Hence, the pre-processing of Vis–NIR spectra is necessary in order to extract soil property-related information (Stenberg and Viscarra Rossel, 2010). As there is no standard pre-processing technique which works on all spectral data (Stenberg and Viscarra Rossel, 2010), it is recommended to always test various techniques and to choose the one which performs best for the respective data. Several studies, therefore, have compared a rather high number of pre-processing methods. Scattering and other effects attributed to within-sample variance can be addressed by repeated measurements of replicate samples (e.g. Pimstein et al., 2011). Altogether, Vis–NIR soil spectrometry has been used on many occasions to build SOC prediction models (Jiang et al., 2016; Kuang and Mouazen, 2013; Nocita et al., 2013).
However, the application of Vis–NIR soil spectrometry for SOC determination involves a couple of uncertainties. The required calibration data are determined with standard laboratory analysis, e.g. dry combustion, with associated uncertainties. On the other hand, the spectral measurements are affected by the sample preparation, e.g. drying, sieving, grinding (e.g. Nduwamungu et al., 2009). Furthermore, sensor noise and other spectrometer internal sources (electronic and mechanical) can affect the measurements (Schwartz et al., 2011). Finally, these two uncertain data sources are related by a regression model. And the model building procedure involves a couple of error sources itself. The development of robust models requires a resampling procedure to determine the model parameters and to avoid overfitting; the applied resampling method impacts model performance (e.g. Molinaro et al., 2005; Beleites et al., 2005). Further aspects that impact model performance are the available dataset in concordance with the applied sampling design, the handling of outliers, spectral pre-processing, and last but not least the model evaluation procedure. In most studies dealing with SOC prediction from Vis–NIR spectra, no clear statement about input data uncertainties or their handling is made. The reported prediction errors only refer to the model building procedure, while uncertainties from laboratory measurements are neglected. Commonly, only a single SOC measurement per soil sample is available, and in spectrometric laboratory measurements, the general approach consists in averaging the multiple measured spectra of one sample to one spectrum, which is then used for model building (Ge et al., 2011; Stevens et al., 2013; Viscarra Rossel et al., 2003). However, the number of measurements used to gain one averaged spectrum differs between studies. Jiang et al. (2016), for example, averaged 10 measurements to receive one spectrum, while Volkan Bilgili et al. (2010) and Wang et al. (2014) used four measurements. This difference is also assumed to have an influence on the uncertainties contained in the input data.
Overall, to allow for comparison between studies, in terms of predictive uncertainty in % SOC, a modelling procedure is required that deals with the propagation of the input data uncertainties. For discussion of the general concept, please refer to Jansen (1998); for applications in soil modelling, compare, for example, Heuvelink (1999) and Poggio and Gimona (2014). Although the problem of the involved uncertainties in Vis–NIR spectrometry is well-known (e.g. Gholizadeh et al., 2013; Nduwamungu et al., 2009; Mortensen, 2014), implementations of uncertainty propagation in Vis–NIR spectrometric modelling are lacking.
2.1 The Static Fertilization Experiment Bad Lauchstädt
The soil samples were taken at the LTFE site Static Fertilization Experiment in Bad Lauchstädt in central Germany (Körschens and Pfefferkorn, 1998). Positioned at 51∘24′ N, 11∘53′ E and with an altitude of 113 m a.s.l. (Körschens and Pfefferkorn, 1998), the climate is characterized by a mean annual precipitation of 470–540 mm and an average mean annual temperature of 8.5–9.0 ∘C. The soil type was characterized as a Haplic Chernozem developed from loess (Altermann et al., 2005) with a soil texture of 21.1±1.2 % clay, 72.1±1.7 % silt, and 6.9±1.9 % sand (Dierke and Werban, 2013). Saturated water conductivity and air capacity are medium to high in the topsoil (Altermann et al., 2005). The Static Fertilization Experiment was initialized in 1902 by Schneidewind and Gröbler and is about 4 ha in size (Merbach and Schulz, 2013). Its objective is to investigate the impact of organic and mineral fertilization on soil fertility as well as yield and quality of crops (Körschens and Pfefferkorn, 1998; Schulz, 2017). The experiment includes eight subfields with a width from 25.2 to 28.5 m and a length of 190 m which are each divided into 18 plots that are treated with different mineral and organic fertilizer as well as planted with different crops following a crop rotation (Körschens and Pfefferkorn, 1998). The plots of subfields 4 and 5 are additionally split into 5 smaller subplots.
2.2 Sampling design
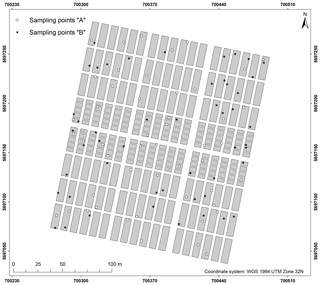
A total of 100 soil samples were taken at the soil surface (0–10 cm) in September 2016. The exact location of the sampling points was determined by a differential GPS/GNSS Leica Viva GS08. It was decided to sample at precise point locations instead of taking samples representative of LTFE plots to allow for a direct comparison with spectrometric field measurements for area-wide regionalization (not included in this study). The sampling points were determined beforehand by two sampling designs. Based on the LTFE treatment factors and per-plot soil archive data including Corg, Ntot, plant-available P, plant-available K (both with double lactate extract method (VDLUFA, 2012), and pH (Fig. 1), both designs strived to select a dataset of 50 samples representative of the soil variability of the entire LTFE. Categorical and continuous data first entered a factor analysis for mixed data (FAMD) performed with R package FactoMineR (Lê et al., 2008) to allow for further joint analysis. For design A the LTFE plots were then grouped by a k-means cluster analysis. R package NbClust (Charrad et al., 2014) automatically determines the optimal number of clusters making use of 30 indices. In the end, 10 plots were randomly selected from each of the resulting five clusters, making a total of 50 plots to be sampled. For design B, the Kennard–Stone algorithm was applied with R package prospectr (Kennard and Stone, 1969; Stevens and Ramirez Lopez, 2014); 50 LTFE plots were selected involving 5 repetitions of the algorithm to reduce inter-point dependence. Finally, one sampling point was randomly selected from each of the 50 LTFE plots for design A and B based on a 5 cm × 5 cm raster. Plot margins of 1.5 m (3 m between plots) were excluded. Figure 2 shows the location of the obtained 100 soil samples.
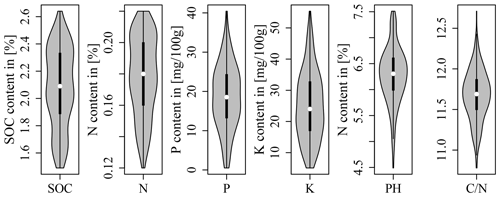
Figure 1Soil archive data of the LTFE measured from 2004 to 2007 (reports of the experimental station Bad Lauchstädt 2004–2007; unpublished data).
2.3 Laboratory measurements
The soil samples were air-dried, sieved, and ground prior to carbon measurements with dry combustion. A high-end elemental analyser vario EL cube CN was used. Measurements were repeated in three replicate samples. Carbon measurements were taken as SOC due to negligibly small carbonate contents (below detection limit). The Vis–NIR contact measurements were performed on air-dried and sieved (2 mm) samples in July 2017, using Veris® Vis–NIR spectrophotometer by Veris Technologies, Inc. (hereinafter called Veris) containing an Ocean Optics USB4000 instrument (200 to 1100 nm) and a Hamamatsu TG series mini-spectrometer (1100 to 2200 nm, resolution 6 nm). The device was warmed up for at least 20 min before performing measurements. All measurements were taken in a dark room to prevent daylight from affecting the outcome. The soil samples were scanned from the top. Before and between soil sample measurements, Veris was calibrated using four Avian Technologies Fluorilon™ grayscale standards. Each soil sample was divided into three subsamples filled into Petri dishes (Schott Duran Petri dishes; Duran Group, Mainz, Germany). These replicate samples were not related to the three replicate samples used for SOC measurements. For each replicate sample, six spectra were gained by measuring each replicate sample three times, rotating it by 90∘, and then measuring it three times again. This procedure resulted in 18 spectra for each soil sample. Internally the spectrometer averaged 25 scans for each spectrometer reading (spectrometer setting).
2.4 Spectral pre-processing
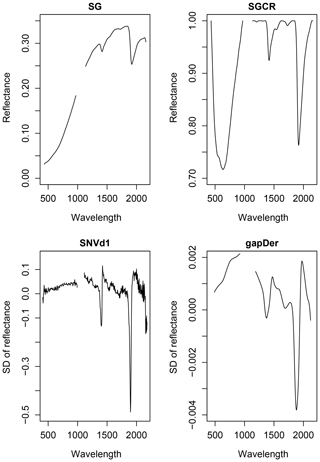
Veris is equipped with two spectrometers. At the beginning and end of their respective wavelength ranges noise occurs in the measurements. Therefore, the spectra between these wavelengths (1000 to 1100 nm) had to be removed. Additionally, the spectra were cut at the beginning (402 nm) and the end (2220 nm). A number of pre-processing methods were tested to enhance the information regarding SOC in the Vis–NIR spectra. The spectra were tested for outliers using R package mvoutlier (Filzmoser and Gschwandtner, 2018). For this procedure, a principal component analysis (PCA) is performed, using then the first two obtained PCs for outlier detection with function aq.plot. Out of the tested pre-processing methods, four different combinations are shown in this study in order to demonstrate their impact on model performance. Their application resulted in spectra with different wavelength ranges (Table 1) and different appearance (Fig. 3). These pre-processing techniques include the Savitzky–Golay algorithm (SG), the continuum removal (CR), the standard normal variate (SNV), the first derivative (d1), and the gap-segment algorithm (gapDer). All pre-processing methods for this study were conducted using R package prospectr (Stevens and Ramirez Lopez, 2014). The SG algorithm fits a polynomial regression on the spectral data to find the derivative at a centre point i of a defined smoothing window (w) (Savitzky and Golay, 1964). CR can be seen as a spectra normalization technique which enables the comparison of different absorption characteristics from a mutual baseline. The continuum is calculated by linear interpolation of the reflectance spectrum's maxima. We implemented CR following Stevens and Ramirez Lopez (2014) by calculating
for , with xi and ci being the initial and the continuum reflectance values at wavelength i of a set of p wavelengths. ϕi then gives the continuum-removed reflectance value. SNV is a scatter-corrective pre-processing method (Barnes et al., 1989). The basic formula is as follows:
where a0 is the measured spectrum's average value which shall be corrected, and a1 is the sample spectrum's standard deviation. xorg is the original spectrum and xcorr the corrected spectrum after applying SNV. In this study, SNV operates row-wise, and each observation is processed on its own (Stevens and Ramirez Lopez, 2014). d1 is calculated by the finite difference method, i.e. the difference between two subsequent data points xi and xi−1 (Eq. 3):
where is the value of the first derivative at the ith wavelength (Rinnan et al., 2009). The downside of using derivative spectra is their tendency to increase noise so that smoothing of the data is required (Stevens and Ramirez Lopez, 2014). With the gapDer, smoothing is performed under a chosen segment size (s) and then a derivative follows (Stevens and Ramirez Lopez, 2014).
Table 1Combinations of pre-processing techniques used in this study; w is window size, s segment size.

2.5 Error propagation
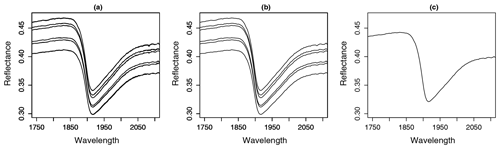
A problem occurring in every model building process is uncertainty propagation. Uncertainties of the input data and model result in uncertainties in the output (Brown and Heuvelink, 2006). Uncertainties in the input data are caused by errors in data acquisition (e.g. measurement errors) as well as variation in the data themselves (e.g. within-sample variability) (Heuvelink, 1999). For this study, there are two different sources for errors in data acquisition: the measurement of the spectral data and the measurement of the SOC content of the soil samples. In order to investigate the influence of these errors, different datasets were built in this study. Figure 4 gives an overview. From the measured Vis–NIR spectra, three different spectral data variants were created (Fig. 4, step 1). For the first variant, all 18 spectra were retained. The inclusion of all 18 spectra reveals the influence of the error implemented in the spectral measurements as well as the influence of the within-sample variability. For the second variant, the three measurements obtained before and after sample rotation were averaged separately resulting in 6 spectra per sample showing the influence of within-sample variability (replicate measurements). For the third data variant, all 18 spectra were averaged to 1 mean spectrum per sample, removing the influence of the measurement error as well as the within-sample variability. The different spectra obtained through this procedure can be seen in Fig. 5; only parts of the spectra are depicted in order to show their differences. The three different spectral data variants were then pre-processed with the methods from Table 1 (Fig. 4, step 2), resulting in 12 different spectral datasets (Fig. 4, step 3). These were then combined with single and averaged SOC values in step 4 so that altogether 24 datasets were obtained (Fig. 4, step 5). In order to compare the two sampling designs, this procedure was carried out for the 50 soil samples labelled “A” and “B” and also for the complete set of soil samples. In this way, three different soil sample sets (“A”, “B” and “all” samples) were obtained.
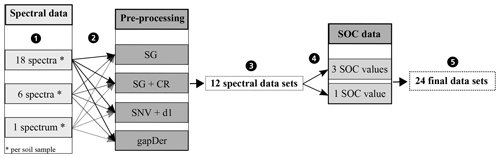
Figure 4Datasets to investigate the uncertainty propagation. SG − Savitzky–Golay, CR − continuum removal, SNV − standard normal variate, d1 − 1st derivative, gapDer − gap-segment algorithm.
2.6 Model building and validation
Regression models were built using partial least square regression (PLSR). Out of the many algorithms, PLSR is seen as a standard method for spectral calibration and prediction (Mouazen et al., 2010; Viscarra Rossel et al., 2006b). For recent applications to predict SOC from Vis–NIR soil spectra, see e.g. Liu et al. (2018) and Yang et al. (2019). PLSR is described in detail by Martens and Næs (1989) and Naes et al. (2002). It incorporates characteristics from PCA and multiple regression (Abdi, 2007). The concept behind PLSR is to seek a small number of linear combinations (components or latent factors) obtained from the measured spectral data and to use them in the regression equation to predict SOC instead of the initial values (Martens and Næs, 1989; Naes et al., 2002). These components are constructed so that they account for most of the variance in the measured spectral data (X) and the SOC content (Y), and at the same time they maximize the correlation between X and Y. In other words, PLSR leads to the covariance between X and Y being maximized (Bjørsvik and Martens, 2008; Wehrens, 2011).
In order to receive a robust model, it is important not to include too many components in model building as this will lead to overfitting (Hastie et al., 2009; Kuhn and Johnson, 2013). On the other hand, the inclusion of too few components comprises the risk of building an underfitted model which is too simple to cover the variability existing in the soil spectral data (Naes et al., 2002). The selection of the optimal number of components is hereinafter referred to as model tuning. In order to receive a robust model, resampling is commonly applied for model validation. But resampling can also be used for model tuning to receive robust tuning parameters (Guio Blanco et al., 2018; Hastie et al., 2009; Kuhn and Johnson, 2013). For small datasets, k-fold cross-validation (CV) is recommended (Hastie et al., 2009).
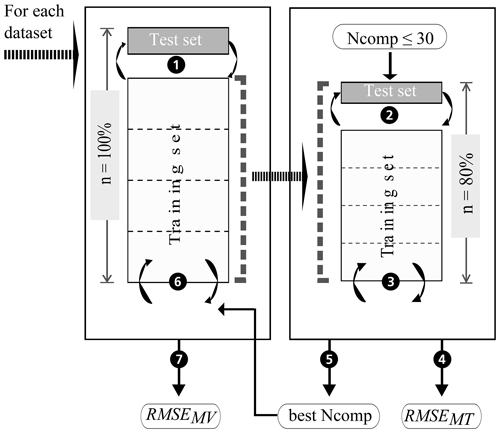
In this study, model building, model validation, and model tuning were implemented using a nested CV approach (Fig. 6; e.g. Varma and Simon, 2006, and Guio Blanco et al., 2018). The CV for model validation and tuning consisted of a repeated k-fold group CV. In order to calculate reliable error measures, the subdivision of the spectral data into the folds had to account for repeated scans and replicate measurements per sample. Accordingly, all spectra for one sample were assigned to the same fold during k-fold CV, i.e. k-fold group CV. Furthermore, to allow for comparison of the models built on behalf of the 24 datasets (Fig. 4), the created folds coincide for all datasets; the data of certain sample IDs were always assigned to the same fold ID. For the model validation CV, two further aspects were taken into account that were neglected for the model tuning CV. The group CV was adapted to also guarantee that neighbouring points of ≤5 m distance were assigned to the same fold to avoid spatial autocorrelation and error measures that are too optimistic. Furthermore, the response variable's density distribution was taken into account during fold creation, i.e. a stratified CV. Overall, a nested repeated k-fold group CV was applied. Five repetitions of a 5-fold group CV were conducted in this case. Kuhn and Johnson (2013) recommend 5-fold CV as it can increase the precision of the prediction while maintaining a small bias.
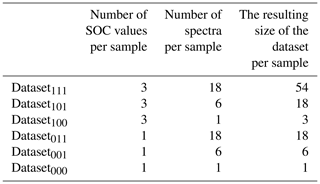
Figure 6 shows the various steps of the modelling procedure involving repeated 5-fold group CV for model tuning (right box) and validation (left box). In the process, the dataset (n=100 %) is randomly subdivided into 5 folds of equal size (step 1). One of the 5 folds is held out as a test set and the other four are used as the training set and partitioned again into 5 folds for model tuning (step 2). The optimal number of components (best Ncomp) is then determined by computing a PLSR on the resampled data, testing 1 to 30 components (step 3) and calculating the repeatedly 5-fold cross-validated RMSE of model tuning (RMSEMT) corresponding to each number of components (step 4). The latter was implemented with the trainControl() function of R package caret (Kuhn, 2017). The optimal number of components (step 5) is then used in model building (step 6). The resulting model's test set RMSE of model validation (RMSEMV) is determined in step 7. The whole procedure is repeated until all folds have once been used as the test set to have a simple 5-fold group CV. A repeated 5-fold group CV means that the model tuning CV and model validation CV each have to be rerun according to the number of repetitions. Finally, the performance of the models built with the 24 datasets is compared based on their RMSEMV mean and interquartile range. Table 2 displays the respective dataset size per soil sample. The resulting datasets and models were named according to the following scheme: Dataset with the SOC measurement error (x1), the spectral measurement error (x2), and the within-sample variability (x3). A value of 1 indicates that the respective error is included in the model; a value of 0 shows that the error was removed beforehand by averaging the data.
3.1 Soil organic carbon content
Figure 7 compares the distribution of the SOC content of the three soil sample sets to the LTFE archive data (Fig. 1). A Mann–Whitney U test was applied. The statistics of the data are given in Table 3. In all cases, no significant difference between the respective dataset and the archive data could be found. This shows that all soil sample sets used in this study were representative of the SOC variability in the LTFE. Nevertheless, the SOC distribution of A and B samples differed. The A samples contained more samples representing higher SOC values, whereas the B samples showed a higher representation of lower SOC values. The violin plots of all three datasets do not resemble the archive violin plot very much. The plots for A samples show higher and lower SOC values than the archive data; B samples share the same minimum value with the archive data but display slightly higher SOC values. This difference is likely due to the fact that the archive data were obtained from compound samples; i.e. a number of distributed soil samples were taken per LTFE plot and mixed before they were subjected to soil laboratory analysis.
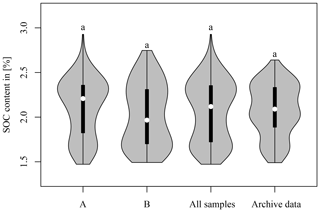
Figure 7Soil organic carbon (SOC) content of the three soil sample sets A (left), B (middle), and all (middle) and of archive data measured from 2004 to 2007 (right). The thin line shows the 95 % confidence interval, the bar the interquartile range, and the dot the median. Mann–Whitney U test was used to compare A, B, and all samples to the archive data. The three soil sample sets were not compared among each other.
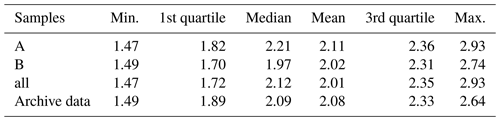
Table 3Statistics of soil organic carbon in percent for the three different soil sample sets and the per-plot soil archive data.
3.2 Comparison of datasets and pre-processing methods
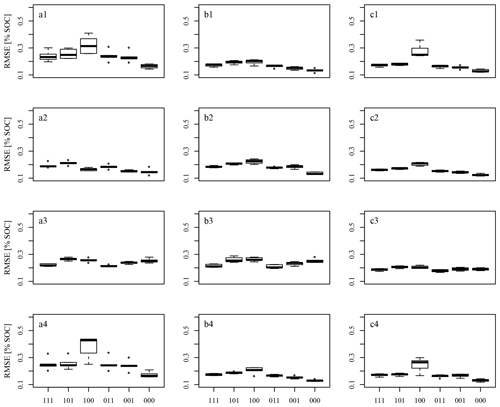
Figure 8 shows the box plots of the RMSEMV. The results of the six datasets corresponding to different information concerning SOC values and spectra (Table 2) are displayed in one plot. The results according to the various pre-processing methods (compare Fig. 4) are displayed in figure lines 1 to 4, and the results of the models built from the data corresponding to A samples, B samples, and all samples are shown in figure columns a, b, and c. As 5-fold CV with five repetitions was performed, five RMSEMV test sets are shown in each box plot.
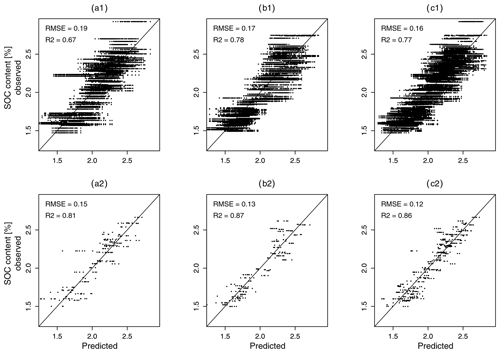
Figure 9Comparison of predicted and observed soil organic carbon (SOC) values for Dataset111 (a1 to c1) and Dataset000 (a2 to c2) for five repetitions with the corresponding best pre-processing (SGCR for data A and all data, SG for data B); (a) shows results for A samples, (b) for B samples, and (c) for all samples. The depicted RMSE and R2 values refer to the mean of five repetitions.
Table 4R2 model performance values from Vis–NIR applications to predict SOC.
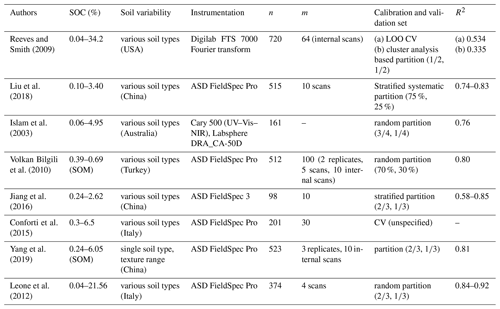
n, number of samples; m, averaged spectral measurements per sample; LOO CV, leave-one-out cross-validation.
As expected, the dataset of three SOC replicate measurements with one averaged spectrum (Dataset100) resulted in low model performance, as the within-sample variance concerning SOC could not be explained by the contained predictor information; the input data uncertainty propagated through the model building process. This model performance was impaired in some cases by Dataset101, which combined the three SOC measurements with six replicate spectral measurements (Fig. 8b1, a2, a3, b3, c3). It seems that the within-sample variation concerning soil spectra was somehow able to compensate for the within-sample variability concerning SOC in the model building process, although replicate measurements did not match. Considering the dataset with 18 spectra and 3 SOC measurements (Dataset111), model performance improved even further. In contrast to this, we found the expected pattern while only one SOC measurement was considered: model performance results display an increase of RMSE values from Dataset000 to Dataset001 to Dataset011 due to the fact that more spectral variance was related to the same target information concerning SOC. This applies to three of the four spectral pre-processing variants (SG, SGCR, gapDer), while SNVd1 pre-processing displays an unexpected pattern with datasets including replicate measurements and multiple scans even outperforming those with averaged data. Overall SGCR resulted in the best model performance for data A (Fig. 8a2) and all samples (Fig. 8c2), while SG pre-processing resulted best for data B (Fig. 8b1). However, the latter does not apply for Dataset000, where gapDer pre-processing resulted in the best model performance with RMSEMV=0.13.
The overall best pre-processing methods in this study were the combination of SG and CR as well as SG alone. SG was used successfully by many authors before for spectral pre-processing. CR was used by, for example, Viscarra Rossel et al. (2016) and Loum et al. (2016) with acceptable success. The combination of SG and CR could not be found in literature, though. SNV was applied before by other authors in order to remove baseline effects (Knadel et al., 2015; Minasny et al., 2011; Viscarra Rossel et al., 2006a). The pre-processing technique d1 was found to lead to poorer model results and rather unexpected performance patterns in this study. The former may have its cause in the tendency of d1 to increase noise (Leone et al., 2012; Stevens and Ramirez Lopez, 2014). We do not have an explanation for the latter, though. Leone et al. (2012) suggested the usage of SG in combination with d1 to solve the problem. For the usage of gapDer no comparison could be found in the literature.
Comparing the mean RMSEMV, the models built on samples B resulted in better model performance than those built on samples A with the exception of Dataset100. The Mann–Whitney U test did not show a significant difference. The A samples, as well as B samples, seem to represent the archive data in an adequate way. Nevertheless, the difference in the distribution of SOC values of A and B samples may have led to the observed different predictive capability in certain SOC value ranges. However, whether this difference is the reason for the better performance of the B models cannot be stated with certainty.
Comparing the results of Dataset111 with those of Dataset000 shows how the inclusion of all input data uncertainties impaired model performance. It can be seen that a model without error propagation (Dataset000) achieved a mean RMSEMV of 0.12 % SOC and a mean R2 of 0.86 using the pre-processing method which delivered the best results. A model with error propagation (Dataset111), on the other hand, reached a mean RMSEMV of 0.16 % SOC and an R2 of 0.77. This is further illustrated in Fig. 9 and could be expected, as Dataset000 contained no input data uncertainties. The RMSEMV values, therefore, only correspond to the model building process. Overall, the best model performance which did not consider error propagation corresponded to a mean RMSEMV of 0.12 % SOC (R2=0.86). This model performance was impaired by ΔRMSEMV=0.04 % SOC while considering input data uncertainties (ΔR2=0.09), and by ΔRMSEMV=0.12 (ΔR2=0.17) considering an inappropriate pre-processing. The effect of the sampling design amounted to a ΔRMSEMV of 0.02 % SOC (ΔR2=0.05). Overall, the additional accounting of neighbouring sample locations during fold division not only for model validation CV but also for model tuning CV might still improve the performance of all models. This is currently not implemented in the applied R package caret. We will, therefore, opt for other implementations in future studies.
Model performance values between studies that use Vis–NIR spectral information to predict soil properties are often compared to one another without mentioning the underlying range of the target variable, the variability of the measured soils, the applied sampling design, measurement protocol, validation approach, or applied instrumentation. Often, this information is not even provided by the respective studies. However, all of this has an impact on the calculated measures of model performance. The listed studies used a different number of scans and replicate samples to calculate an averaged spectrum to predict SOC. Often, it is not specified whether the measurements refer to instrument internal scans, repeated external scans, or replicate measurements. As a consequence, the error implemented in the respective spectral input data must be assumed to be different. Pimstein et al. (2011) proposed a number of 3–5 replicate measurements as standard protocol for measuring Vis–NIR spectra of soil samples under laboratory conditions. Figure 5b indicated the high impact of within-sample variance determined by the measurements of replicate samples, whereas the effect of the repeated scans per replicate was comparatively small (compare Fig. 5a and b). We dried and sieved the samples before spectral measurements but did not grind them to a fine powder. The latter might reduce the spectral variance in replicate measurements, but the benefit of Vis–NIR spectroscopy as a fast and inexpensive method would be reduced. One might argue that samples had to be ground for SOC analysis, anyway. However, this requires a tiny fraction of the large amount that would have to be ground for Vis–NIR measurements. In addition, comparison to measurements under field conditions would be further distorted while grinding the samples for laboratory measurements. In none of the studies listed in Table 4 was the error in SOC measurements mentioned to be considered during model building. Also, in most studies the available dataset was randomly parted into calibration and validation set, using different data proportions for the two sets. Jeong et al. (2017) and Beleites et al. (2005) showed that different validation strategies led to different error values. As shown in Fig. 8, the input data uncertainty had a major influence on model performance. Accordingly, the applied measurement protocol should be reported with complete details.
This study addressed the impact of various data and modelling aspects on model performance with a focus on the propagation of input data uncertainties. Overall, the best model performance which did not consider uncertainty propagation corresponded to a mean RMSEMV of 0.12 % SOC (R2=0.86). This model performance was impaired by ΔRMSEMV=0.04 % SOC considering input data uncertainties (ΔR2=0.09) and by ΔRMSEMV=0.12 % SOC (ΔR2=0.17) considering an inappropriate pre-processing. The effect of the sampling design amounted to a ΔRMSEMV of 0.02 % SOC (ΔR2=0.05).
Overall, the applied nested k-fold group CV approach can be recommended in general. Furthermore, this study showed that it is of uttermost importance to clarify which information is contained in the reported error values. We, therefore, emphasize the necessity of a transparent and precise documentation of the measurement protocol, the model building, and validation procedure, including the calculation of the error measure, in order to assess model performance in a comprehensive way and allow for comparison between publications. Particularly, when Vis–NIR spectrometry is used for soil monitoring, the aspect of uncertainty propagation in the involved modelling procedure becomes essential.
The data of this study are available from https://doi.org/10.17605/OSF.IO/TN4KU (Ließ, 2019).
ME conducted spectral lab measurements, data analysis, and manuscript writing. IM provided access to the LTFE site as well as corresponding information and the archive data. UW provided lab facilities and supervised the spectral measurements. ML was responsible for sampling setup and data acquisition, conceptual embedding of the manuscript, manuscript writing, and revision during the review process.
The authors declare that they have no conflict of interest.
We are grateful to the support of our colleagues from the UFZ departments of Soil System Science, Community Ecology, Monitoring and Exploration Technologies, and Computational Landscape Ecology for support during the field campaign and the consequent sample preparation and laboratory analysis.
This paper was edited by Nikolaus J. Kuhn and reviewed by three anonymous referees.
Abdi, H.: Partial Least Square Regression – PLS-Regression, in: Encyclopedia of Measurement and Statistics, edited by: Salkind, N., ThousandOaks (CA), Sage., 2007.
Adamchuk, V. I. and Viscarra Rossel, R. A.: Development of On-the-Go Proximal Soil Sensor Systems, in: Proximal Soil Sensing. Progress in Soil Science, edited by: Viscarra Rossel, R. A., McBratney, A., and Minasny, B., 15–28, Springer, Dordrecht, 2010.
Altermann, M., Rinklebe, J., Merbach, I., Körschens, M., Langer, U., and Hofmann, B.: Chernozem – Soil of the Year 2005, J. Plant Nutr. Soil Sc., 168, 725–740, https://doi.org/10.1002/jpln.200521814, 2005.
Barnes, R. J., Dhanoa, M. S., and Lister, S. J.: Standard Normal Variate Transformation and De-Trending of Near-Infrared Diffuse Reflectance Spectra, Appl. Spectrosc., 43, 772–777, 1989.
Beleites, C., Baumgartner, R., Bowman, C., Somorjai, R., Steiner, G., Salzer, R., and Sowa, M. G.: Variance reduction in estimating classification error using sparse datasets, Chemometr. Intell. Lab., 79, 91–100, https://doi.org/10.1016/j.chemolab.2005.04.008, 2005.
Ben-Dor, E., Irons, J. A., and Epema, A.: Soil Spectroscopy, in: Manual of Remote Sensing, edited by: Rencz, A., 111–188, J. Wiley & Sons, Inc., NewYork, 1999.
Ben Dor, E., Ong, C., and Lau, I. C.: Reflectance measurements of soils in the laboratory: Standards and protocols, Geoderma, 245–246, 112–124, https://doi.org/10.1016/j.geoderma.2015.01.002, 2015.
Bjørsvik, H.-R. and Martens, H.: Data Analysis: Calibration of NIR Instruments by PLS Regression, in Handbook of Near-Infrared Analysis, edited by: Burns, D. A. and Ciurczak, E. W., 189–205, 2008.
Brown, J. D. and Heuvelink, G. B. M.: Assessing Uncertainty Propagation through Physically Based Models of Soil Water Flow and Solute Transport, in: Encyclopedia of Hydrological Sciences, edited by: Anderson, M. G., 1181–1195, Wiley, Chicester, UK, 2006.
Charrad, M., Ghazzali, N., Boiteau, V., and Niknafs, A.: NbClust: An R Package for Determining the Relevant Number of Clusters in a Data Set, J. Stat. Softw., 61, 1–36, 2014.
Conforti, M., Castrignanò, A., Robustelli, G., Scarciglia, F., Stelluti, M., and Buttafuoco, G.: Laboratory-based Vis-NIR spectroscopy and partial least square regression with spatially correlated errors for predicting spatial variation of soil organic matter content, Catena, 124, 60–67, https://doi.org/10.1016/j.catena.2014.09.004, 2015.
Croft, H., Kuhn, N. J., and Anderson, K.: On the use of remote sensing techniques for monitoring spatio-temporal soil organic carbon dynamics in agricultural systems, Catena, 94, 64–74, https://doi.org/10.1016/j.catena.2012.01.001, 2012.
Dalal, R. C. and Henry, R. J.: Simultaneous Determination of Moisture, Organic Carbon, and Total Nitrogen by Near Infrared Reflectance Spectrophotometry1, Soil Sci. Soc. Am. J., 50, 120, https://doi.org/10.2136/sssaj1986.03615995005000010023x, 1986.
Dierke, C. and Werban, U.: Geoderma Relationships between gamma-ray data and soil properties at an agricultural test site, Geoderma, 199, 90–98, https://doi.org/10.1016/j.geoderma.2012.10.017, 2013.
Filzmoser, P. and Gschwandtner, M.: Package “mvoutlier”: Multivariate outlier detection based on robust methods, R package version 2.0.9, available at: https://cran.r-project.org/web/packages/mvoutlier/mvoutlier.pdf (last access: 18 September 2019), 2018.
Ge, Y., Morgan, C. L. S., Grunwald, S., Brown, D. J., and Sarkhot, D. V.: Comparison of soil reflectance spectra and calibration models obtained using multiple spectrometers, Geoderma, 161, 202–211, https://doi.org/10.1016/j.geoderma.2010.12.020, 2011.
Gholizadeh, A., Boruvka, L., Sbaerioon, M., and Vasat, R.: Visible, near-infrared, and mid-infrared spectroscopy applications for soil assessment with emphasis on soil organic matter content and quality: State-of-the-art and key issues, Appl. Spectrosc., 67/12, 1349–1362, 2013.
Guio Blanco, C. M., Brito Gomez, V. M., Crespo, P., and Ließ, M.: Spatial prediction of soil water retention in a Páramo landscape: Methodological insight into machine learning using random forest, Geoderma, 316, 100–114, https://doi.org/10.1016/j.geoderma.2017.12.002, 2018.
Hastie, T., Tibshirani, R., and Friedman, J. H.: The Elements of Statistical Learning, 2nd Edn., Springer, New York, 2009.
Heuvelink, G. B. M.: Propagation of error in spatial modelling with GIS, in: Geographical Information Systems, edited by: Longley, P. A., Goodchild, M. F., Maguire, D. J., and Rhind, D. W., 207–217, New York, John Wiley & Sons, 1999.
Islam, K., Singh, B., and McBratney, A. B.: Simultaneous estimation of several soil properties by ultra-violet, visible, and near-infrared reflectance spectroscopy, Aust. J. Soil Res., 41, 1101–1114, https://doi.org/10.1071/SR02137, 2003.
Jansen, M.: Prediction error through modelling concepts and uncertainty from basic data, Nutr. Cycl. Agroecosys., 50, 247–253, https://doi.org/10.1023/A:1009748529970, 1998.
Jeong, G., Choi, K., Spohn, M., Park, S. J., Huwe, B., and Ließ, M.: Environmental drivers of spatial patterns of topsoil nitrogen and phosphorus under monsoon conditions in a complex terrain of South Korea, PLoS One, 12, 1–19, https://doi.org/10.1371/journal.pone.0183205, 2017.
Jiang, Q., Chen, Y., Guo, L., Fei, T., and Qi, K.: Estimating Soil Organic Carbon of Cropland Soil at Different Levels of Soil Moisture Using VIS-NIR Spectroscopy, Remote Sens., 8, 755, https://doi.org/10.3390/rs8090755, 2016.
Johnson, M. G.: Soil carbon sequestration: Quantifying this ecosystem service, Present. Oregon Soc. Soil Sci. Annu. Meet., 28–29 February 2008, Newport, OR, 2008.
Kennard, R. W. and Stone, L. A.: Computer Aided Design of Experiment, Technometrics, 11, 137–148, 1969.
Knadel, M., Thomsen, A., Schelde, K., and Greve, M. H.: Soil organic carbon and particle sizes mapping using vis-NIR, EC and temperature mobile sensor platform, Comput. Electron. Agr., 114, 134–144, https://doi.org/10.1016/j.compag.2015.03.013, 2015.
Körschens, M. and Pfefferkorn, A.: Bad Lauchstädt – The Static Fertilization Experiment and other Long-Term Field Experiments, UFZ – Umweltforschungszentrum Leipzig-Halle GmbH, 1998.
Kuang, B. and Mouazen, A. M.: Non-biased prediction of soil organic carbon and total nitrogen with vis e NIR spectroscopy, as affected by soil moisture content and texture, Biosyst. Eng., 114, 249–258, https://doi.org/10.1016/j.biosystemseng.2013.01.005, 2013.
Kuhn, M.: Package “caret”: Classification and regression training, Version 6.0-84, available at: https://cran.r-project.org/web/packages/caret/caret.pdf (last access: 18 September 2019), 2017.
Kuhn, M. and Johnson, K.: Applied Predictive Modeling, Springer, New York Heidelberg Dordrecht London, 2013.
Lal, R.: Soil Carbon Sequestration Impacts on Global Climate Change and Food Security, Science, 304, 1623–1627, https://doi.org/10.1126/science.1097396, 2004.
Lê, S., Josse, J., and Husson, F.: FactoMineR: An R Package for Multivariate Analysis, J. Stat. Softw., 25, 1–18, https://doi.org/10.1016/j.envint.2008.06.007, 2008.
Leone, A. P., Viscarra Rossel, R. A., Amenta, P., and Buondonno, A.: Prediction of Soil Properties with PLSR and vis-NIR Spectroscopy?: Application to Mediterranean Soils from Southern Italy, Curr. Anal. Chem., 8, 283–299, https://doi.org/10.2174/157341112800392571, 2012.
Ließ, M.: DATA: Error propagation in spectrometric functions of soil organic carbon, OSF Home, https://doi.org/10.17605/OSF.IO/TN4KU, 2019.
Liu, Y., Zhou, S., Zhang, G., Chen, Y., Li, S., Hong, Y., Shi, T., Wang, J., and Liu, Y.: Application of spectrally derived soil type as ancillary data to improve the estimation of soil organic carbon by using the Chinease soil Vis-NIR spectral library, Remote Sens., 10, 1–16, https://doi.org/10.3390/rs10111747, 2018.
Lorenz, K. and Lal, R.: Soil Organic Carbon – An Appropriate Indicator to Monitor Trends of Land and Soil Degradation within the SDG Framework?, edited by: Starke, S. M. and Ehlers, K., Umweltbundesamt, Dessau-Roßlau,, 2016.
Loum, M., Diack, M., Ndour, N. Y. B., and Masse, D.: Effect of the Continuum Removal in Predicting Soil Organic Carbon with Near Infrared Spectroscopy (NIRS) in the Senegal Sahelian Soils, Open J. Soil Sci., 6, 135–148, https://doi.org/10.4236/ojss.2016.69014, 2016.
Martens, H. and Næs, T.: Multivariate Calibration, JohnWiley & Sons, Chichester, UK, 1989.
McBratney, A. B., Stockmann, U., Angers, D. A., Minasny, B., and Field, D. J.: Challenges for Soil Organic Carbon Research, in Soil Carbon, Progress in Soil Science, edited by: Hartemink, A. E. and McSweeney, K., p. 57, Springer International Publishing, Switzerland, 2014.
Meersmans, J., Van Wesemael, B., and Van Molle, M.: Determining soil organic carbon for agricultural soils?: a comparison between the Walkley & Black and the dry combustion methods (north Belgium), Soil Use Manage., 25, 346–353, https://doi.org/10.1111/j.1475-2743.2009.00242.x, 2009.
Merbach, I. and Schulz, E.: Long-term fertilization effects on crop yields, soil fertility and sustainability in the Static Fertilization Experiment Bad Lauchstädt under climatic conditions 2001–2010, Arch. Agron. Soil Sci., 59, 1041–1057, https://doi.org/10.1080/03650340.2012.702895, 2013.
Minasny, B., McBratney, A. B., Bellon-Maurel, V., Roger, J.-M., Gobrecht, A., Ferrand, L., and Joalland, S.: Removing the effect of soil moisture from NIR diffuse reflectance spectra for the prediction of soil organic carbon, Geoderma, 167–168, 118–124, https://doi.org/10.1016/j.geoderma.2011.09.008, 2011.
Molinaro, A. M., Simon, R., and Pfeiffer, R. M.: Prediction error estimation: a comparison of resampling methods, Bioinformatics, 21, 3301–3307, 2005.
Mortensen, P.: Myth: A partial least squares calibration model can never be more precise than the reference method…, NIR News, 25, 20–22, 2014.
Mouazen, A. M., Kuang, B., De Baerdemaeker, J., and Ramon, H.: Comparison among principal component , partial least squares and back propagation neural network analyses for accuracy of measurement of selected soil properties with visible and near infrared spectroscopy, Geoderma, 158, 23–31, https://doi.org/10.1016/j.geoderma.2010.03.001, 2010.
Naes, T., IsakssonT., Fearn, T., and Davies, T.: A User Friendly Guide to Multivariate Calibration and Classification, NIR Publications, Chichester, 2002.
Nieder, R. and Benbi, D. K.: Carbon and Nitrogen in the Terrestrial Environment, Springer, the Netherlands, 2008.
Nduwamungu, C., Ziadi, N., Parent, L.-E., Tremblay, G. F., and Thuriès, T.: Opportunities for, and Limitations of, Near Infrared Reflectance Spectroscopy Applications in Soil Analysis: A Review, Can. J. Soil Sci., 89, 531–541, 2009.
Nocita, M., Stevens, A., Noon, C., and Van Wesemael, B.: Prediction of soil organic carbon for different levels of soil moisture using Vis-NIR spectroscopy, Geoderma, 199, 37–42, https://doi.org/10.1016/j.geoderma.2012.07.020, 2013.
Pilorget, C., Fernando, J., Ehlmann B., Schmidt, F., and Hiroi, T.: Wavelength dependence of scattering properties in the VIS–NIR and links with grain-scale physical and compositional properties, Icarus, 267, 296–314, 2016.
Pimstein, A., Notesco, G., and Ben-Dor, E.: Performance of Three Identical Spectrometers in Retrieving Soil Reflectance under Laboratory Conditions, Soil Sci. Soc. Am. J., 75, 746, https://doi.org/10.2136/sssaj2010.0174, 2011.
Poggio, L. and Gimona, A.: National scale 3D modelling of soil organic carbon stocks with uncertainty propagation – An example from Scotland, Geoderma, 232–234, 284–299, 2014.
Reeves, J. B. and Smith, D. B.: The potential of mid- and near-infrared diffuse reflectance spectroscopy for determining major- and trace-element concentrations in soils from a geochemical survey of North America, Appl. Geochem., 24, 1472–1481, https://doi.org/10.1016/j.apgeochem.2009.04.017, 2009.
Rinnan, Å., van den Berg, F., and Engelsen, S. B.: Review of the most common pre-processing techniques for near-infrared spectra, TrAC – Trend Anal. Chem., 28, 1201–1222, https://doi.org/10.1016/j.trac.2009.07.007, 2009.
Savitzky, A. and Golay, M. J. E.: Smoothing and Differentiation of Data by Simplified Least Squares Procedures, Anal. Chem., 36, 1627–1639, https://doi.org/10.1021/ac60214a047, 1964.
Schulz, E.: Static Fertilization Experiment Bad Lauchstädt, available at: http://www.ufz.de/index.php?en=37010 (last access: October 2018), 2017.
Schwartz, G., Eshel, G., and Ben-Dor, E.: Reflectance Spectroscopy as a Tool for Monitoring Contaminated Soils, in: Soil Contamination, edited by: Pascucci, S., InTech, New York, 67–90, https://doi.org/10.5772/23661, 2011.
Stenberg, B. and Viscarra Rossel, R. A.: Diffuse Reflectance Spectroscopy for High-Resolution Soil Sensing, in: Proximal Soil Sensing. Progress in Soil Science, edited by: Viscarra Rossel, R. A., McBratney, A., and Minasny, B., 29–47, Springer, Dordrecht, 2010.
Stenberg, B., Viscarra Rossel, R. A., Mouazen, A. M., and Wetterlind, J.: Visible and Near Infrared Spectroscopy in Soil Science, Adv. Agron., 107, 163–215, https://doi.org/10.1016/s0065-2113(10)07005-7, 2010.
Stevens, A. and Ramirez Lopez, L.: An introduction to the prospectr package, 1–22, available at: http://cran.r-project.org/web/packages/prospectr/vignettes/prospectr-intro.pdf (last access: November 2018), 2014.
Stevens, A., Nocita, M., Tóth, G., Montanarella, L., and van Wesemael, B.: Prediction of Soil Organic Carbon at the European Scale by Visible and Near InfraRed Reflectance Spectroscopy, PLoS One, 8, e66409, https://doi.org/10.1371/journal.pone.0066409, 2013.
Stockmann, U., Adams, M. A., Crawford, J. W., Field, D. J., Henakaarchchi, N., Jenkins, M., Minasny, B., Mcbratney, A. B., Remy, V. De, Courcelles, D., Singh, K., Wheeler, I., Abbott, L., Angers, D. A., Baldock, J., Summers, D., Lewis, M., Ostendorf, B., and Chittleborough, D.: Visible near-infrared reflectance spectroscopy as a predictive indicator of soil properties, Ecol. Indic., 11, 123–131, https://doi.org/10.1016/j.ecolind.2009.05.001, 2011.
Varma, S. and Simon, R.: Bias in error estimation when using cross-validation for model selection, BMC Bioinformatics, 7, 91, https://doi.org/10.1186/1471-2105-7-91, 2006.
VDLUFA: Methodenbuch Band I Die Untersuchung von Böden, in: Das VDLUFA Methodenbuch, VDLUFA-Verlag, Darmstadt, 2012.
Viscarra Rossel, R. A., Walter, C., and Fouad, Y.: Assessment of two reflectance techniques for the quantification of the within-field spatial variability of soil organic carbon, edited by: Stafford, J. and Werner, A., Precision Agriculture. Fourth European Conference on Precsision Agriculture, Wageningen Academic Publishers, Berlin, 697–702, 2003.
Viscarra Rossel, R. A., McGlynn, R. N., and McBratney, A. B.: Determining the composition of mineral-organic mixes using UV-vis-NIR diffuse reflectance spectroscopy, Geoderma, 137, 70–82, https://doi.org/10.1016/j.geoderma.2006.07.004, 2006a.
Viscarra Rossel, R. A., Walvoort, D. J. J., McBratney, A. B., Janik, L. J., and Skjemstad, J. O.: Visible, near infrared, mid infrared or combined diffuse reflectance spectroscopy for simultaneous assessment of various soil properties, Geoderma, 131, 59–75, https://doi.org/10.1016/j.geoderma.2005.03.007, 2006b.
Viscarra Rossel, R. A., Behrens, T., Ben-Dor, E., Brown, D. J., Demattê, J. A. M., Shepherd, K. D., Shi, Z., Stenberg, B., Stevens, A., Adamchuk, V., Aichi, H., Barthès, B. G., Bartholomeus, H. M., Bayer, A. D., Bernoux, M., Böttcher, K., Brodský, L., Du, C. W., Chappell, A., Fouad, Y., Genot, V., Gomez, C., Grunwald, S., Gubler, A., Guerrero, C., Hedley, C. B., Knadel, M., Morrás, H. J. M., Nocita, M., Ramirez-Lopez, L., Roudier, P., Campos, E. M. R., Sanborn, P., Sellitto, V. M., Sudduth, K. A., Rawlins, B. G., Walter, C., Winowiecki, L. A., Hong, S. Y., and Ji, W.: A global spectral library to characterize the world's soil, Earth-Sci. Rev., 155, 198–230, https://doi.org/10.1016/j.earscirev.2016.01.012, 2016.
Volkan Bilgili, A., van Es, H. M., Akbas, F., Durak, A., and Hively, W. D.: Visible-near infrared reflectance spectroscopy for assessment of soil properties in a semi-arid area of Turkey, J. Arid Environ., 74, 229–238, https://doi.org/10.1016/j.jaridenv.2009.08.011, 2010.
Wang, Y., Lu, C., Wang, L., Song, L., Wang, R., and Ge, Y.: Prediction of Soil Organic Matter Content Using VIS/NIR Soil Sensor, Sensors & Transducers, 168, 113–119, 2014.
Wehrens, R.: Chemometrics with R – Multivariate Data Analysis in the Natural Sciences and Life Sciences, edited by: Gentleman, G. P. R. and Hornik, K., Springer-Verlag Berlin Heidelberg, 2011.
Yang, M., Xu, D., Chen, S., Li, H., and Shi, Z.: Evaluation of machine learning approaches to predict soil organic matter and pH using Vis-NIR spectra, Sensors, 19, 1–14, https://doi.org/10.3390/s19020263, 2019.