Machine learning and soil sciences: a review aided by machine learning tools

The application of machine learning (ML) techniques in various fields of science has increased rapidly, especially in the last 10 years. The increasing availability of soil data that can be efficiently acquired remotely and proximally, and freely available open-source algorithms, have led to an accelerated adoption of ML techniques to analyse soil data. Given the large number of publications, it is an impossible task to manually review all papers on the application of ML in soil science without narrowing down a narrative of ML application in a specific research question. This paper aims to provide a comprehensive review of the application of ML techniques in soil science aided by a ML algorithm (latent Dirichlet allocation) to find patterns in a large collection of text corpora. The objective is to gain insight into publications of ML applications in soil science and to discuss the research gaps in this topic. We found that (a) there is an increasing usage of ML methods in soil sciences, mostly concentrated in developed countries, (b) the reviewed publications can be grouped into 12 topics, namely remote sensing, soil organic carbon, water, contamination, methods (ensembles), erosion and parent material, methods (NN, neural networks, SVM, support vector machines), spectroscopy, modelling (classes), crops, physical, and modelling (continuous), and (c) advanced ML methods usually perform better than simpler approaches thanks to their capability to capture non-linear relationships. From these findings, we found research gaps, in particular, about the precautions that should be taken (parsimony) to avoid overfitting, and that the interpretability of the ML models is an important aspect to consider when applying advanced ML methods in order to improve our knowledge and understanding of soil. We foresee that a large number of studies will focus on the latter topic.

1 Introduction

The application of machine learning (ML) techniques in various fields of science has increased rapidly, especially in the last 10 years. Soil science research, in particular, pedometrics, has used statistical models to “learn” or understand from data how soil is distributed in space and time (McBratney et al., 2019). The increasing availability of soil data that can be efficiently acquired remotely and proximally, and freely available open-source algorithms, have led to an accelerated adoption of ML techniques to analyse soil data. Several well-known ML applications in soils science include the prediction of soil types and properties via digital soil mapping (DSM) or pedotransfer functions and analysis of infrared spectral data to infer soil properties. Machine learning analysis of soil data is also used to draw conclusions on the controls of the distribution of the soil.

The definition of what constitutes ML is still contentious or sometimes mistaken. In this work, instead of adding a new argument to differentiate ML from statistical science, we will focus on the view of Jordan and Mitchell (2015), where ML is “lying at the intersection of computer science and statistics”. With respect to artificial intelligence (AI), sometimes we have seen the terms ML and AI used interchangeably. This is understandable confusion since ML is a subset of AI, but not everything related to AI falls in the ML category (e.g. expert systems).

There are concerns that ML application ignores soil science knowledge (Rossiter, 2018) and that the results could be misleading and wrong. Nevertheless, many would find that ML methods can help in the scientific process (Mjolsness and DeCoste, 2001; Rudin and Wagstaff, 2014): observations, empirical and theory-based model development, and simulations of soil processes (Rossiter, 2018). For example, exploration of high-dimensional infrared spectral data helps in understanding the horizonation designation in a soil profile (Fajardo et al., 2016). The process of modelling and validation can be used to formulate a model to explain soil distribution (Brungard et al., 2015). Modelling via ML can also be used to improve our understanding of the causes of soil variation. Results from ML models can inform on which environmental variables control soil distribution. New relationships revealed by ML analysis can help to stimulate ideas, generate hypotheses, and formulate future questions for research (Ma et al., 2019).

This paper aims to provide a comprehensive review of the application of ML techniques in soil science. A quick Google Scholar search of “soil” and “machine learning” resulted in more than 70 000 items, with 16 000 items published in 2018. While we can narrow down a narrative of ML application in a specific research question, such as the application of ML in yield prediction in precision agriculture (Chlingaryan et al., 2018) or DSM, it is an impossible task to manually review all papers on the application of ML in soil science. One ML technique that has not been applied in soil science is topic modelling, a type of quantitative text mining method. Similar to what ML does to numerical data, topic modelling finds patterns in a large collection of text corpora (Blei et al., 2003; Blei, 2012), and it has been used to study the evolution of various disciplines and topics (Zhou et al., 2006; Sugimoto et al., 2011; Wu et al., 2014).

This paper uses topic modelling to analyse the trend in ML application in soil science. The objective is to gain insight into publications of ML applications in soil science; in particular, we will try to answer the following questions.

• Who is using ML, and is the application of ML as ubiquitous as we think?

• Which ML methods are commonly used and how often have they been used?

• In which areas of soil sciences do we use ML, and how are they clustered and related?

• Do advanced ML methods perform significantly better than linear or non-linear statistical approaches?

• Can ML methods simulate soil processes in space and time?

• Can we use ML methods to improve our knowledge and understanding of soil?

Throughout this review, we will refer to models as “simple” or “complex/advanced”, trusting in the readers' criteria. To illustrate that gradient between simple and complex, we considered a linear model (LM) with 2 variables to be simple compared to a LM with 100 variables; a classification and regression tree (CART) with 2 branches to be simple compared to a CART with 100 branches; and finally, a CART with 2 branches to be simple compared with a LM with 100 variables. We also hope that is clear for the reader that a model such as a deep convolutional neural network (CNN) has many parameters; hence, it is more complex than a CART model.

2 Methods

2.1 Article selection

In order to identify the primary group of articles, we used the term “soil `machine learning”' to perform a full-text search in databases from different publishers. We selected the publishers based on (a) our institution having access to full-text articles and (b) that they provide text-mining permission. We limited our search to the English-only literature, without fixing a specific time frame, and completing the search on 1 February 2019. After performing a screening for the relevance of the initial 3044 matches, we decided to narrow down the selection to the articles containing the word “soil” in their title, yielding a total of 322 articles. The final journal names and number of articles are shown in Table A1 in the Appendix.

2.2 Topic modelling

Topic modelling is a probabilistic ML method that aims to discover and annotate large archives of documents with thematic information Blei (2012). By analysing the words contained in a set of documents, these topic modelling algorithms are capable of identifying common themes. These methods allow processing of an arbitrarily large number of articles, which can help to reduce part of the bias introduced by only selecting a manageable subset of documents or by manually assigning documents to topics.

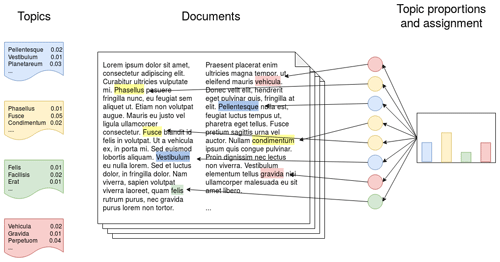
In order to determine in which areas of soil sciences we use ML, we selected an algorithm commonly used in topic modelling called latent Dirichlet allocation (LDA) (Blei et al., 2003) to perform the task of allocating the articles to topics. LDA is a probabilistic model that assumes that a number of topics exist in a document collection and each topic is represented by a distribution of words. Each document is represented by a distribution over topics, and each word is a sample over each topic's vocabulary (Fig. 1). For more details about the LDA, we refer the reader to Blei (2012).

Figure 1 Collection of topics with distribution of words (left), document distribution over topics (histogram, right), and words sampled from the topics' vocabularies (circles). The topics, words, and assignment are for illustrative purposes. Adapted from Blei (2012).

Before modelling the topics, we pre-processed the documents in order to reduce the noise of the unstructured texts. We (a) removed stop words (common words such as “from” and “are”), (b) generated bi- and tri-grams, which are groups of two or three words which commonly appear together in the text (e.g. “remote sensing”, “particle size distribution”), and (c) removed extremely uncommon (that appear in less than five documents) and common words (that appear in more than 50 % of the documents), which do not help to differentiate between topics.

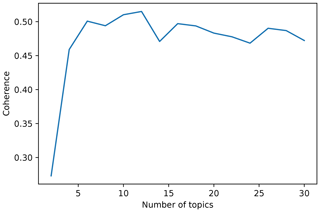
The LDA algorithm is capable of learning different topics to which each document is assigned given the words that constitute it. The first challenge is to find the optimal number of topics, which has to be general enough to capture similarities between articles but with some degree of specificity in order to have a manageable and sensible group of topics. That balance between generality and specificity is key to generating topics that are semantically interpretable by a human (Stevens et al., 2012). One of the measures that is highly correlated with human interpretation of the topics is topic coherence (Stevens et al., 2012). We estimated a coherence measure proposed by Röder et al. (2015) (referenced as CV in their paper) for different models trained with an increasing number of topics, from 2 to 30. CV is an aggregated measure which combines a normalised point-wise mutual information coherence measure, cosine vector similarity, and a Boolean sliding window of size 110. It ranges from 0 to 1, 1 being the highest coherence. Other parameters of the LDA algorithm, such as the threshold of the probability above which a topic is considered, and the number of training iterations, were set to 0.2 and 1000, respectively, after performing a parameter grid search.

2.3 Text extraction

In order to identify the information required to answer our questions, we used a combination of named-entity recognition and rule-based matching. To extract the MODEL entities, we used a list of modelling methods from the Outline_of_machine_learning Wikipedia article in addition to other algorithms that are commonly used in soil sciences and that were not present in the list (e.g. Cubist). After extracting the MODEL entities, we proceeded to extract the abbreviations used to reference those models. In order to extract the abbreviations, we relied on the commonly seen pattern of writing model names followed by their corresponding abbreviation (e.g. “we used a random forest model (RF)”). By extracting the abbreviations we expected to discriminate between (a) models used to generate the results reported in the articles and (b) models mentioned to give context to the studies. Extracting abbreviations also allowed us to capture variations of models not present in our original list (e.g. BART for bagged regression trees in Fig. 2).

Figure 2 Excerpt from one of the reviewed articles showing named entities recognised as models. Note that the word “bagged” is not recognised, but the abbreviation “bart” is.

2.4 Implementation

We performed all our analysis in Python, using the libraries gensim v3.6.0 (Řehůřek and Sojka, 2010) and the MALLET package (McCallum, 2002) for the topic modelling and spacy v2.1.0a6 (Matthew and Honnibal, 2017) for the named entity recognition.

3 Results and discussion

3.1 Who is using machine learning methods?

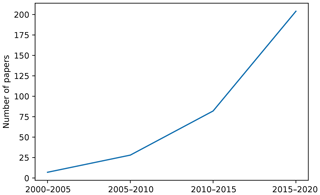
The first questions related to the current status of the ML literature in soil sciences can be answered after correctly organising all the articles' metadata. Regarding the general usage of ML methods, in our review, we observed an expected increment in time in the number of publications using ML to model different aspects of soils (Fig. 3). This increment is most likely due to a combination of increasing computational power and accessibility to high-performance computers, increasing availability of data (e.g. remote sensing) (Jordan and Mitchell, 2015), and the increasing interest in “data science”. It is also confounded with the overall increase in the number of publications, which was estimated in 2015 at nearly 2.5 million new publications per year (Ware and Mabe, 2015).

Figure 3 Distribution in time of the articles used in this review.

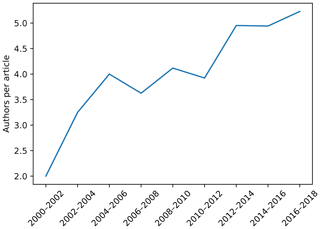
Besides the temporal trend in publishing, we were also interested in how ubiquitous the application of ML methods is. Fig. 4 shows the number of institutions per country (log₁₀) that appeared listed as affiliations in the analysed articles. ML techniques in the context of soil sciences are used in many countries around the world, but are mostly concentrated in developed countries. This is due to the inseparable relationship between science, technology, and development (Sagasti, 1973), which is also related to what is usually called the “digital divide” (Rossiter, 2018). Inter-institutional collaboration could be an important aspect of closing this gap (Sonnenwald, 2007). Similarly to what is happening in many disciplines (Sonnenwald, 2007), we observed an increase in the number of co-authors per article (Fig. 5), which might be a good sign if we avoid bad practices like “helicopter science” (Minasny and Flantis, 2018).

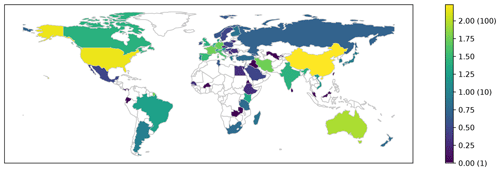
Figure 4 Total number (log₁₀) of institutions per country that participated in articles included in this review. Numbers between brackets are the real number of publications. Outlined countries have zero occurrences.

Figure 5 Evolution of the number of authors per publication. Mean values per time period.

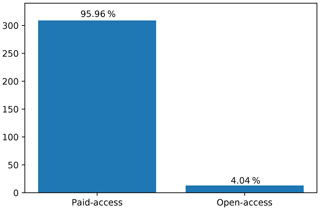
The advance of a discipline is not only measured by the number of publications. Dissemination of knowledge is a key component of research and open access (OA) has been recognised as an optimal solution since it is in the best interests of all stakeholders involved in the process (Björk, 2017). In the application of ML in soil sciences, the proportion of OA publications is very low (Fig. 6). This number is in line with the overall OA presence in science (Björk, 2017) but on the opposite side of the general trend in ML, where scientists prefer AO (Hutson, 2018).

3.2 Most used methods

From the huge variety of ML models available, we found over 100 different variants that have been applied in the soil sciences. From those, most have been applied experimentally in one or two papers, and just a handful are consistently used. Fig. 7 depicts the evolution of some selected models. There is an overall increase in the usage of all the models but, proportionally, it is possible to see a decrease in the usage of some models such as support vector machines (SVM), multivariate adaptive regression spline (MARS), and CART, giving way to more advanced alternatives such as random forest (RF). The adoption of the latter has an accelerated growth, and it has been used in a diversity of topics, including mapping and spectroscopy. The appearance of deep learning is also noticeable, which at the moment has only been used in a few publications related to mapping and spectroscopy.

3.3 Main topics

As we mentioned in Sect. 2.2, in order to find the optimal number of topics present in the corpora, we trained models with an increasing number of topics (from 2 to 30) and we plotted the evolution of the CV coherence (Fig. 8). From this curve it is possible to select the number of topics that yield the highest coherence, which in this case is 12.

These 12 topics correspond to main soil areas detected by the LDA algorithm where ML is applied. We extracted the most relevant words for each of the 12 topics and we examined the titles of the more relevant papers to identify suitable “topic names”. The 12 identified areas were the following.

Remote sensing.

Articles heavily based on remote sensing (Grunwald et al., 2015; Xu et al., 2017; Zhang et al., 2018b). Articles related to salinity were also assigned to this group since most of them use remote sensing techniques (Khadim et al., 2019; Zhang et al., 2019).

Soil organic carbon.

Articles related to soil organic carbon (SOC) cycles and dynamics and its relationship with the environment. Carbon stocks in different ecosystems, with particular emphasis on grasslands and topsoil (Rial et al., 2017; Liu et al., 2018; Song et al., 2018; Wang et al., 2018a).

Water.

Articles mostly focused on soil water content and its changes over time (Ahmad et al., 2010; Coopersmith et al., 2014; Greifeneder et al., 2018; Han et al., 2018). Other articles in this category are related to soil temperature and CO₂ fluxes (Xing et al., 2018; Oh et al., 2019; Warner et al., 2019; Zeynoddin et al., 2019). All these articles comprise measurements made by “stations”.

Contamination.

Articles addressing problems related to heavy metals, soil pollution, and bio-availability (Costa et al., 2017; Reeves et al., 2018; Wu et al., 2013).

Methods (ensembles).

Articles with a focus on model ensembles such as RF (Blanco et al., 2018; Tziachris et al., 2019).

Erosion/parent material.

Articles focused on soil formation processes, specifically additions and losses by deposition and erosion, respectively (Geissen et al., 2007; Märker et al., 2011; Martinez et al., 2017). Since soil formation depends on the parent material, articles aiming to characterise it were also included in this category (Kheir et al., 2008; Lacoste et al., 2011).

Methods (NN, SVM).

Articles with a focus on methods such as neural networks (NN) and SVM (Kovačević et al., 2010; Farfani et al., 2015; Hanna et al., 2007).

Spectroscopy.

This topic is related to proximal soil sensing covering different light wavelength sections, from microwave to infrared to gamma (Heggemann et al., 2017; Butler et al., 2018; Xie and Li, 2018).

Modelling (classes).

Articles focused on the modelling, especially mapping, of categorical soil properties based on their relationship with environmental covariates (Mansuy et al., 2014; Camera et al., 2017; Dharumarajan et al., 2017; Massawe et al., 2018). In this category it is also possible to find articles related to the use of conventional soil maps, especially spatial disaggregation of polygons (Subburayalu et al., 2014; Vincent et al., 2018; Flynn et al., 2019).

Crops.

This group of articles focused not merely on soil, but also on its interaction within the soil–plant continuum. Water and nutrient availability in order to ensure crop yields is a key component of this topic (Karandish and Šimŭnek, 2016; Ivushkin et al., 2018; Khanal et al., 2018; Leenaars et al., 2018).

Physical.

Articles related to the physical properties of soils, including texture and bulk density (Bondi et al., 2018; Naderi-Boldaji et al., 2019), and how they affect aspects of soil such as water retention and flow (Koestel and Jorda, 2014; Gao et al., 2018).

Modelling (continuous).

Articles focused on the modelling, especially mapping, of continuous soil properties based on their relationship with environmental covariates, from regional to continental scales (Henderson et al., 2005; Dai et al., 2014; Poggio et al., 2016; Padarian et al., 2019a; Caubet et al., 2019). In this category it is also possible to find articles related to pedotransfer functions (Dobarco et al., 2019).

Figure 6 Number of articles published under paid and open access.

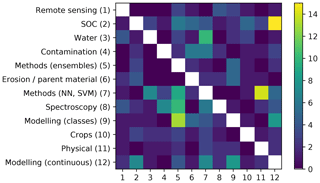
These topics are not completely independent and they share some commonalities. For instance, Fig. 9 shows an overlap between Topic 12 (Modelling continuous properties) and 9 (Modelling classes) since both are related to mapping using environmental covariables. Both topics are also related to Topic 3 (Water) since its articles usually have a spatial component. Something similar occurs between Topics 8 (Spectroscopy) and 1 (Remote sensing) since both are related to spectral data.

.

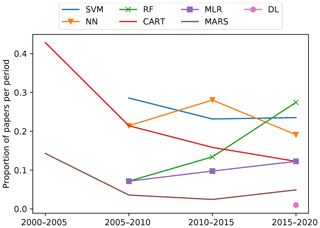
Figure 7 Evolution of model usage in time. SVM: support vector machines; NN: neural networks; RF: random forest; CART: classification and regression trees; MLR: multiple linear regression; MARS: multivariate adaptive regression spline; DL: deep learning

Figure 8 Coherence by number of topics used to train a LDA model.

Besides the shared features between topics, given that LDA is a probabilistic model, articles also contain features related to more than one topic; i.e. they talk about more than one topic (Fig. 10). For instance, many of the articles related to SOC are also related to soil modelling and mapping (Deng et al., 2018; Wang et al., 2018b; Gomes et al., 2019; Keskin et al., 2019).

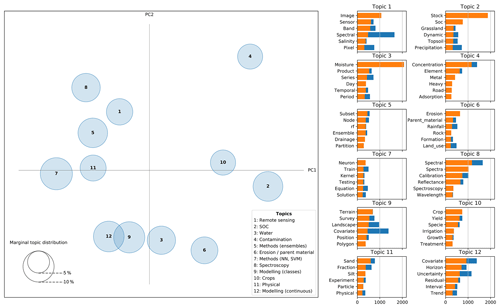
Figure 9 Inter-topic distance map. Dimension reduction via Jensen–Shannon divergence (Lin, 1991) and principal coordinate analysis. Top-6 more relevant words per topic. Complete bars (blue + orange) correspond to overall term frequency and shaded bars (orange) correspond to term frequency within the selected topic.

3.4 Performance of machine learning models

Our review shows that more advanced modelling techniques usually yield better results compared with simpler approaches. In one of the more extensive comparisons, Sirsat et al. (2018) compared 76 different algorithms, where ensembles of extremely randomised regression trees ranked first when predicting soil fertility indices. Other comparative studies also showed a consistent higher performance of ML methods (NN, SVM, RF) over simpler approaches (principal component regression, partial least squares regression (PLSR), multiple linear regression (MLR), k-nearest neighbours) in applications such as spectroscopy (Viscarra-Rossel and Behrens, 2010; Morellos et al., 2016) and DSM (Brungard et al., 2015; Taghizadeh-Mehrjardi et al., 2015; Camera et al., 2017; Jeong et al., 2017). Most studies mention that the superiority of these algorithms is given by their capability to deal with complex non-linearities present in the data. Moreover, the better performance of more advanced ML methods is reported in studies related to the prediction of continuous properties and classes.

Regarding the connection between performance and model usage (Sect. 3.2), we observed that some simpler methods such as MLR, despite their lower performance compared to more advanced models, are very popular. This is expected for statistical models since they have a long tradition in science. On the other hand, we also observed a natural tendency of leaving some models behind despite being used for a long time. For instance, PLSR is very popular and has been used since the 1980–1990s but, when used in the studies included in this review (mostly published post the 2000s), very few studies use it as their main algorithm and, instead, it is used in comparative studies where it is outperformed by more advanced models.

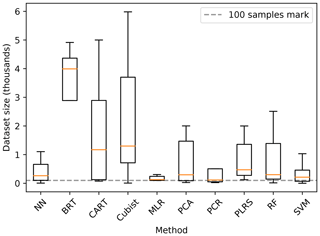
It is worth noting that the final performance is not solely dependent on the selected modelling method. Advanced methods like NN have a big number of parameters to fit, especially in the context of deep learning. In order to correctly fit those parameters, from a computational and statistical point of view, the size of the dataset is an essential factor (Jordan and Mitchell, 2015). Padarian et al. (2019b) show that a deep CNN trained using a large dataset (around 20 000 soil samples) outperformed methods such as PLS and Cubist when predicting soil properties from spectral data. Using the same method but training on a significantly smaller dataset (390 soil samples), the CNN yielded the worst results.

There is no clear rule on how big a dataset should be, especially because it certainly depends on the complexity of the underlying problem, but the relationship between dataset size and performance has been shown in many studies, using what is usually known as “learning curves” (Catlett, 1991; Shavlik et al., 1991; Cortes et al., 1994; Perlich et al., 2003; Somarathna et al., 2017). During our review, we observed that the dataset size varied greatly depending on the ML methods (Fig. 11).

Considering that ML models could generate a similar solution to a linear model (e.g. a single-rule tree), it should not be a problem to use any method for any dataset size. However, the main difficulty is that training a complex ML model is not a trivial task, especially to avoid overfitting and to obtain a good generalisation, which becomes challenging in the presence of small datasets (i.e. training and test datasets). Even if a researcher can overcome the training process, it is probable that a simpler model can yield similar results.

3.5 Space–time modelling

Compared with the spatial component of soil variation, which is prominent in the topics found using the LDA algorithm (Sect. 3.3), the number of studies that address the spatio-temporal dynamics of soil properties using ML methods is still limited. Our findings agree with the review by Grunwald (2009), who characterised studies covering the years 2007 and 2008. A big proportion of studies that deal with the temporal dynamics of soil properties are related to soil–water interactions, as shown in Topic 3 of our topic detection analysis (Fig. 9).

We found three main approaches to deal with the temporal variation of soil.

Temporal extrapolation.

The studies generate models for a specific time step, including one or more predictors that vary in time to then apply that fitted model to another time step (e.g. Grinand et al., 2017).

Subtraction.

The studies model two or more time steps independently followed by a change analysis. For instance, Schillaci et al. (2017a) and Zhang et al. (2018b) subtracted the maps of the modelled properties from 2 different years to compute the change in SOC concentration and pH, respectively.

Dynamics.

Studies that model the actual dynamics of a soil property based on some mechanistic or semi-mechanistic method. Stumpf et al. (2018) created yearly land-use covers for 8500 km² in Switzerland using a combination of Landsat 5–7–8 and field land-use observations in order to model the SOC dynamics based on the conversion regimes from their land-use sequence patterns (Watson et al., 2014).

Despite there being ML algorithms that have the capacity to capture 4-D structures (e.g. convolutional recurrent neural networks), we did not find studies using ML to continuously model space and time simultaneously. We think the main reason is that soil observations are usually sparse in space–time (Grunwald, 2016) and that it is not possible to fulfill the dataset size requirements of such models. That is the reason why we mostly find studies that use a mechanistic or semi-mechanistic approach.

Figure 10 Co-occurrence between the two most likely topics per document. Values correspond to the number of papers.

Figure 11 Boxplot of reported dataset sizes grouped by method. Outliers were removed.

3.6 Uncertainty assessment

Uncertainty assessment is an important requirement for any model, especially if the predictions are going to be used to guide decision-making. In this review, 24 % of the studies, among most topics, present uncertainty assessment or mention the importance of considering it (Fig. 12).

In this review, a major contributor to the promotion of uncertainty assessment in soil modelling is the GlobalSoilMap project (Arrouays et al., 2014) which, through specification developed by the DSM scientific community, recommends an uncertainty assessment of all their products. This is evident from Fig. 12, where topics related to DSM show a relatively high proportion of articles mentioning or reporting uncertainty. In the GlobalSoilMap specifications, the proposed uncertainty assessment method is the use of bootstrapping when training the model (Stine, 1985), effectively making predictions with many models trained with subsets of the original data to then estimate the 90 % prediction interval (e.g. Castro-Franco et al., 2017; Ma et al., 2017). Another approach is the use of quantile regression (Koenker and Bassett Jr., 1978) to estimate the complete conditional distribution of the prediction. This method has been recently applied in some DSM studies (Vaysse and Lagacherie, 2017; Sirsat et al., 2018; Cao et al., 2019). Less common approaches are the use of the fuzzy k-means with the extragrades (Tranter et al., 2010) algorithm, which defines areas within the covariate space, with different levels of uncertainty, where a new observation (to be predicted) can be placed, and the use of Bayesian optimisation approaches (Snoek et al., 2015; Gal and Ghahramani, 2016).

Figure 12 Number of articles per topic that report or mention “uncertainty”. Percentage represents the proportion of total articles per topic.

4 General discussion

4.1 Interpretability

Based on our findings, it is possible to state that, in general, ML methods have shown superior performance over more traditional methods in terms of predictive power. We now address the last questions from the aims of this paper — does an advanced model provide new insights that improve our knowledge and understanding of soils?

In order for a human to understand the decisions made by the model, the model has to be interpretable. The motivations for interpretability are varied, including trust, causality, transferability, informativeness, and fairness (in ethical terms) (Lipton, 2016). In our review, researches usually associate advanced ML models with low interpretability. For instance, Brungard et al. (2015) assigned multiple models to different groups according to their complexity, with NN and SVM categorised as difficult to interpret compared to MLR or CART. Beguin et al. (2017) also mention the lower interpretability of ML models compared with an explicit geostatistical model. Because how to measure interpretability is usually not well defined, there are also contradictory opinions. For instance, RF is mostly considered in the category of low interpretability (Brungard et al., 2015; Were et al., 2015; Taghizadeh-Mehrjardi et al., 2016; Deng et al., 2018), but its use is also sometimes justified due to its ease of interpretability via the use of variables of importance (Jeong et al., 2017).

It is important to clearly define the goal of a modelling exercise. If we want to obtain the model with the greatest accuracy in order to solve a specific problem, maybe interpretability should not be an important factor. If we consider a) that nature is a complex combination of non-linear phenomena and b) the limited capacity of humans to understand non-linear relationships (Doherty and Balzer, 1988), by requiring our model to have complete transparency we are limiting its capability. However, it is important to corroborate that the model is a valid generalisation of the studied phenomenon. If our goal is to obtain new insights, it is important to consider that interpretability goes hand in hand with prior knowledge and biases and that we could be optimising an algorithm to present misleading but plausible explanations (Lipton, 2016).

4.1.1 How can we increase interpretability?

A common conclusion reported by authors of the reviewed papers is that the selection of the most informative or relevant predictors before training the model can increase interpretability (Xiong et al., 2014; Prasad et al., 2018; Wang et al., 2018a; Keskin et al., 2019), although some authors do not recommend selection of predictors based on the researchers' knowledge since it could lead to biased and suboptimal model performance (Brungard et al., 2015; Keskin et al., 2019). This discordance leads to a large range in the number of the predictors used, with some extreme cases using more than 200 (Xiong et al., 2014; Keskin et al., 2019).

NN are some of the most performing models but, given the complexity of their operation, they are usually labelled as “black-box” models. In consequence, many authors have focused on trying to provide frameworks to interpret the knowledge extracted by these models. For instance, Bau et al. (2017) dissected a CNN to understand how different layers work and which features they favour by visualising their (neurons) activation map. Rauber et al. (2017) used the activation maps projected into a 2-D space in order to visualise and identify confusion zones, outliers, and clusters in the internal representations learned by the model.

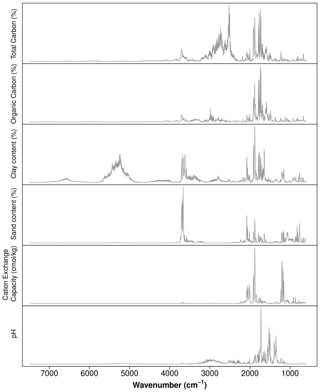
In soil sciences, one of the reported methods to interpret ML models is to assess the importance of the variables used, usually derived from the number of times they have been used in the rules generated by tree-like models (Henderson et al., 2005; Martin et al., 2014; Schillaci et al., 2017b; Khanal et al., 2018). Another method to assess the relative influence of predictors in tree-like models is to estimate the average reduction of the error at each split of the tree, for all the predictors (Friedman, 2001). Another alternative, in the context of soil mapping, is to map the rules generated by the model to identify their spatial context or to map where important predictors were used (Bui et al., 2006). For CNN, by feeding simulated data to a trained model, Ng et al. (2019) explored the most important wavelengths used when predicting multiple soil properties from soil spectral data using a sensitivity analysis. The logic behind their analysis is that modifying unimportant wavelengths should not affect the prediction. By plotting the variance for the predictions by wavelengths it is possible to unveil the most important areas of the spectrum (Fig. 13).

Figure 13 Sensitivity analysis of CNN model prediction as a function of wavelength. Average variance of predictions by wavelength. This analysis allows us to explore the most important wavelengths in a CNN model. Adapted from Ng et al. (2019).

Interpretability is an important concept that should be revisited, since it is neither absolute nor static; hence, a specific model cannot be simply labelled as interpretable or not. Linear models can quickly become unintelligible as we add more variables (Lou et al., 2012), and methods to better understand complex models such as NN are constantly being developed (Bau et al., 2017; Montavon et al., 2018; Zhang et al., 2018a).

4.2 New good practices

Thanks to the effort of some groups to rescue soil legacy data (Arrouays et al., 2017) and cheaper and faster methods to analyse soil samples, there are more soil data available than ever before. This data availability not only allows us to use new ML algorithms, which usually require more observations, but also opens the door to new ways to train those models. An important part of model development is validation. The literature traditionally recommends that an independent, unseen (by the model) dataset should be used as validation (Kohavi, 1995). In practice, the data is usually partitioned into training and validation datasets. A more stable solution is the use of k cross-validation where the dataset is partitioned into k groups, where k−1 groups are used for training and 1 groups for validation, repeating the training k times, each with a different validation group. When data availability is a limitation, researchers resort to techniques such as n cross-validation or “leave-one-out” validation to make the most of the available data (Stevens et al., 2008; Pasini, 2015).

A new generation of models based on NN has been introduced in the later years, which has revolutionised many fields. Deep learning (DL) models, consisting of multiple hidden layers of neurons, have many parameters (from hundreds to millions) which need to be fitted in the training process. This is the reason why they usually need access to large sample sizes. A second characteristic of these models is that they have a considerable number of hyper-parameters. Hyper-parameters are parameters that are not learned from the data during the training phase and include things like the number of iterations during the training, learning rate, layer parameters, or number of layers. A common practice when training DL models is to split the original dataset into three sub-datasets: training, validation, and test. The training dataset is used to learn the parameters, the validation dataset to compare models fitted with different hyper-parameters in order to find the optimal combination, and the test dataset as the independent, unseen data.

In soil sciences, ML algorithms are usually trained using the traditional train–validation split or cross-validation (Keskin et al., 2019; Liang et al., 2019), or even no validation (Feng et al., 2019), except for some studies based on DL or with an engineering background (e.g. Reale et al., 2018), including some of our publications on the use of DL for DSM (Padarian et al., 2019c) or soil spectroscopy (Padarian et al., 2019b, a), which use a train–validation–test split. Considering the increasing size of datasets, we think soil scientists should transition towards the implementation of some DL practices such as dataset split and hyper-parameter optimisation (Bergstra and Bengio, 2012; Snoek et al., 2012), not only for NN, but also for any algorithm that has hyper-parameters. Some potential candidates are random forest, Cubist, classification and regression trees, and support vector machines. Most of the implementations of these algorithms have sensible default hyper-parameters, but some studies report an important impact of them in their results (Mutanga et al., 2012; Lu et al., 2018). For general hyper-parameter tuning strategies, we refer the reader to Bergstra and Bengio (2012) for simple strategies such as grid or random search. For an in-depth report of hyper-parameter tuning and its effects in the context of random forest, we refer the reader to Probst et al. (2019).

4.3 Commercial ML applications

This work explores the use of ML in soil sciences by exploring the current scientific literature, but use of ML extends beyond research and companies are very welcoming to this technology, especially in applications such as computer vision, speech recognition, natural language processing, and robot control (Jordan and Mitchell, 2015). It is not hard to imagine a commercial application of approaches such as soil properties prediction using vis-NIR spectroscopy, either in the laboratory or the field. While in research there are some transparency requirements, including describing the methods and data used, companies are usually very secretive about their methods since they are a trade secret that gives them a competitive advantage. Considering that lack of transparency, how can we be sure that the predictions of their models are good? There is not a unique answer, but it should include at least some uncertainty assessment (as discussed in Sect. 3.6) and information about the range of soils used during training.

In terms of reporting soil types coverage, different approaches can be applied. A simple, perhaps overconfident method can be to report the geographical extent from where the soil samples used during training were collected (e.g. Tomasella et al., 2000; Børgesen and Schaap, 2005) or a broad soil classification based on the soil characteristics such as “sandy soils” (e.g Schaap and Bouten, 1996 and Shaw et al., 2000). A better approach, based on the covariate space of the samples used during training, is fuzzy k-means with extragrades, which has the benefit of describing both coverage and uncertainty levels.

Even if uncertainty levels and coverage are reported, another factor to consider is how much we should trust in companies and their reports. Especially for applications involving public funding, but generally as a consumer protection measure, these type of products should be certifiable in the same way many soil laboratories are. A usual approach is the use of reference materials (Dybczyński et al., 1979; Pueyo et al., 2001; Ahmed et al., 2017), which should be consistent with the model coverage reported. The properties measured in the reference materials should fall within the prediction interval produced by the model, with a confidence defined for each application.

5 Conclusions and recommendations

Aided by a topic modelling approach, we were able to review the status of ML in soil sciences. We observed a general increase in the adoption of ML methods in time, mostly concentrated in developed countries. This gap is probably due to the link between science, technology, and development. We believe that proper inter-institutional collaboration plans should be put in place in order to close this gap.

By using topic modelling, we identified 12 categories of studies where ML is commonly used, namely remote sensing, soil organic carbon, water, contamination, methods (ensembles), erosion and parent material, methods (NN, SVM), spectroscopy, modelling (classes), crops, physical, and modelling (continuous). The final topic model successfully captured relationships between topics such as modelling of continuous and categorical soil properties, and water, given that all these topics share a spatial component.

We also found that advanced ML methods usually perform better than simpler approaches thanks to their capability to capture non-linear relationships. However, it is important to note that more advanced methods usually require more data and that some precautions should be taken in order to avoid obtaining misleading results. Considering parsimony is always advised, if only a small, simple dataset is available, we recommend using a simple model. This also applies to the number of predictors. In consequence, according to many authors of the reviewed articles, it is better to use meaningful predictors instead of relying on the model capabilities to “select the best variables” in order to improve interpretability.

Interpretability is an important aspect to consider when applying advanced ML methods in order to improve our knowledge and understanding of soil. Simpler methods (e.g. linear models) have been used for a long time and the way of interpreting them is well defined. More advanced methods (e.g. neural networks) are usually considered “black box” models, but that is just a reflection of the current research state and not because it is impossible to interpret them. During our review, we found studies that proposed some solutions to improve their interpretability, and we foresee that a large number of studies will focus on this topic.

Appendix A

Table A1 List of journals by publisher and number of articles that matched the term “soil `machine learning”' in a full-text search.

Acronyms
AI	artificial intelligence
CART	classification and regression tree
DSM	digital soil mapping
LDA	latent Dirichlet allocation
LM	linear model
MARS	multivariate adaptive regression spline
ML	machine learning
MLR	multiple linear regression
NN	neural network
PLSR	partial least squares regression
RF	random forest
SOC	soil organic carbon
SVM	support vector machines