Depth extrapolation of field-scale soil moisture time series derived with cosmic-ray neutron sensing (CRNS) using the soil moisture analytical relationship (SMAR) model

Ground-based soil moisture measurements at the field scale are highly beneficial for different hydrological applications, including the validation of space-borne soil moisture products, landscape water budgeting, or multi-criteria calibration of rainfall–runoff models from field to catchment scale. Cosmic-ray neutron sensing (CRNS) allows for the non-invasive monitoring of field-scale soil moisture across several hectares around the instrument but only for the first few tens of centimeters of the soil. Many of these applications require information on soil water dynamics in deeper soil layers. Simple depth-extrapolation approaches often used in remote sensing may be used to estimate soil moisture in deeper layers based on the near-surface soil moisture information. However, most approaches require a site-specific calibration using depth profiles of in situ soil moisture data, which are often not available. The soil moisture analytical relationship (SMAR) is usually also calibrated to sensor data, but due to the physical meaning of each model parameter, it could be applied without calibration if all its parameters were known. However, its water loss parameter in particular is difficult to estimate. In this paper, we introduce and test a simple modification of the SMAR model to estimate the water loss in the second layer based on soil physical parameters and the surface soil moisture time series. We apply the model with and without calibration at a forest site with sandy soils. Comparing the model results with in situ reference measurements down to depths of 450 cm shows that the SMAR models both with and without modification as well as the calibrated exponential filter approach do not capture the observed soil moisture dynamics well. While, on average, the latter performs best over different tested scenarios, the performance of the SMAR models nevertheless meets a previously used benchmark RMSE of ≤ 0.06 cm³ cm⁻³ in both the calibrated original and uncalibrated modified version. Different transfer functions to derive surface soil moisture from CRNS do not translate into markedly different results of the depth-extrapolated soil moisture time series simulated by SMAR. Despite the fact that the soil moisture dynamics are not well represented at our study site using the depth-extrapolation approaches, our modified SMAR model may provide valuable first estimates of soil moisture in a deeper soil layer derived from surface measurements based on stationary and roving CRNS as well as remote sensing products where in situ data for calibration are not available.

1 Introduction

Soil moisture is a key parameter in the hydrological cycle (e.g. Vereecken et al., 2008, 2014; Seneviratne et al., 2010). It controls several aspects of the environment, such as soil infiltration, runoff dynamics, plant growth, and biomass production, which in turn influence evapotranspiration as well as the climatic conditions on varying spatio-temporal scales (see reviews by e.g. Daly and Porporato, 2005; Vereecken et al., 2008; Seneviratne et al., 2010; Wang et al., 2018). Thus, information on soil water dynamics at the field scale have great importance for various larger-scale hydrological applications ranging from landscape water budgeting to multi-criteria calibration approaches in rainfall–runoff modeling. However, due to the high spatio-temporal variability in soil water content (Famiglietti et al., 2008; Vereecken et al., 2014), which is highest in surface soil layers (Babaeian et al., 2019), measuring field-scale soil moisture and its dynamics proves difficult based on invasive point-scale soil moisture measurement methods as, for example, reviewed in Vereecken et al. (2014) and Babaeian et al. (2019). For instance, the installation of electromagnetic point sensors measuring at a high temporal resolution would require a very large number of sensors to obtain a representative field-scale average (Babaeian et al., 2019). Additionally, sensor networks are not always feasible as agricultural management practices hamper a permanent installation of point sensors (Stevanato et al., 2019). As a consequence, extensive point sensor networks, which allow for the estimation of field-scale soil moisture are often restricted to a rather small number of research-related monitoring sites, such as the Terrestrial Environmental Observatories (TERENO; http://www.tereno.net, last access: 15 September 2024) in Germany (e.g. Zacharias et al., 2011; Bogena et al., 2018; Kiese et al., 2018; Heinrich et al., 2018) or the International Soil Moisture Network (ISMN; Dorigo et al., 2021), which cover sites around the globe.

Kodama et al. (1979), Kodama et al. (1985) and Dorman (2004) suggested the potential of naturally occuring secondary neutrons produced by high-energy cosmic rays for estimating soil and snow water. About a decade ago, Zreda et al. (2008) and Desilets et al. (2010) introduced a methodological framework for soil moisture estimation using cosmic-ray neutrons. The cosmic-ray neutron sensing (CRNS) approach is a non-invasive geophysical method for estimating representative field-scale soil moisture (Schrön et al., 2018b) based on the measurement of cosmic-ray neutrons, which are inversely related to the amount of hydrogen in the vicinity of the neutron detector. As soil water is the largest pool of hydrogen in the footprint of the neutron detector in most terrestrial environments, CRNS allows for the measurement of integrated soil moisture of several hectares around the instrument and the first decimetres of the soil (e.g. Zreda et al., 2008; Desilets et al., 2010; Köhli et al., 2015; Schrön et al., 2017).

Estimating soil moisture using CRNS has a high potential for various hydrological applications, which require soil moisture observations at the field scale. Several studies demonstrate the potential of CRNS-derived soil moisture estimates for, for example, a comparison with satellite-derived soil moisture products, their validation, and the improved calibration of environmental models (e.g. Holgate et al., 2016; Montzka et al., 2017; Iwema et al., 2017; Duygu and Akyürek, 2019; Dimitrova-Petrova et al., 2020). Besides stationary CRNS probes for the retrieval of field-scale soil moisture time series, roving CRNS devices have been successfully used in mapping CRNS-derived surface soil moisture in even larger areas with instruments mounted on vehicles (e.g. McJannet et al., 2017; Schrön et al., 2018a; Vather et al., 2019), and Fersch et al. (2018) illustrate potential synergies between CRNS, airborne radar, and in situ point sensor networks for soil moisture estimation across spatial scales. Due to the sensitivity of CRNS to any hydrogen in the measurement footprint, snow monitoring (e.g. Schattan et al., 2017, 2019; Gugerli et al., 2019), irrigation management (e.g. D. Li et al., 2019), and biomass estimation (e.g. Baroni and Oswald, 2015; Tian et al., 2016; Jakobi et al., 2018; Vather et al., 2020) pose further fields of application and are reviewed in Andreasen et al. (2017).

Although the large areal footprint of the CRNS-instrument allows for the estimation of field-scale integral soil moisture, the CRNS-derived time series lack soil moisture information from greater depths. However, soil moisture at these greater depths becomes highly relevant as soon as the rooting depth of crops or forest extends past the first few decimeters. The maximum rooting depth and, hence, root-zone extent as well as root density along the soil profile vary with vegetation type and biome (e.g. Canadell et al., 1996; Jackson et al., 1996). According to Jackson et al. (1996), on global average across all biomes, 75 % of plant roots occur in the first 40 cm of the soil, which would be largely covered by the CRNS. However, the global average maximum rooting depth and, thus, root-zone depth are about 4.6 m (Canadell et al., 1996), where the rooting depth also depends on prevailing soil hydrological conditions (Fan et al., 2017). Even grassy vegetation and crops can have rooting depths of more than 200 cm (Canadell et al., 1996), thus exceeding the measurement depth of CRNS. Deep roots play a significant role in the water supply of plant ecosystems, especially during dry conditions (Canadell et al., 1996) – that is, through hydraulic redistribution (see, for example, Neumann and Cardon, 2012) or increased root water uptake from deeper soil layers under drought conditions (Maysonnave et al., 2022). Furthermore, plant species influence infiltration and vertical soil moisture patterns through species-dependent root distributions (e.g. Jost et al., 2012) and horizontal soil moisture patterns through species-dependent evapotranspiration and interception rates (e.g. Schume et al., 2003). Hence, field-scale soil water information from the deeper vadose zone that overcomes these smaller-scale heterogeneities can be important for the quantification of water storage variations, potential influences on vegetation dynamics, matter fluxes, and the characterization of the local hydrological cycle.

Given the importance of soil moisture in the deeper root zone, extending CRNS measurements to greater depths is of high importance in broadening the applicability of CRNS for soil water estimations (Peterson et al., 2016). Numerous studies extrapolate surface soil moisture time series to greater depths using different empirical approaches (e.g. Zhang et al., 2017; Li and Zhang, 2021), including regression analyses; machine learning techniques; or other approaches, such as the exponential filter/soil water index (SWI) (Wagner et al., 1999; Albergel et al., 2008). Few studies address the depth extrapolation of field-scale CRNS-derived soil moisture time series (e.g. Peterson et al., 2016; Zhu et al., 2017; Nguyen et al., 2019; Franz et al., 2020) to the shallow root zone (approx. 100 cm) by applying and comparing extrapolation approaches, with the SWI being the most commonly used approach (e.g. Peterson et al., 2016; Dimitrova-Petrova et al., 2020; Franz et al., 2020). All these approaches require reference soil moisture information in the depth of interest to either build an empirical model or calibrate the depth-extrapolated soil moisture time series. This information may not always be available in sufficient quantity and quality. In contrast, the physically based soil moisture analytical relationship (SMAR) (Manfreda et al., 2014), which was applied and modified in recent studies (e.g. Faridani et al., 2017; Baldwin et al., 2017, 2019; Gheybi et al., 2019; Zhuang et al., 2020; Farokhi et al., 2021), allows for the extrapolation of daily surface soil moisture information to a second, lower soil layer by solely relying on soil physical information and a water loss term. This method does not require calibration if the environmental parameters are known.

Against this background, we investigate the potential to depth-extrapolate daily surface soil moisture time series without calibration and thus without the need for reference soil moisture information in the depth of interest by applying the SMAR algorithm at a highly instrumented study site in the TERENO-NE observatory located in the lowlands of north-eastern Germany. While soil physical parameters may be determined from soil samples or directly in situ, the water loss parameter that describes the water loss per unit time from the second soil layer is more difficult to estimate. Therefore, we propose a simple modification of the SMAR algorithm to estimate the water loss term from soil physical characteristics and from the surface soil moisture time series. We first compare the standard SMAR that uses a constant calibrated water loss term (calibrated against in situ reference sensors) with the modified uncalibrated SMAR that uses the estimated water loss term for different depths, down to 450 cm, of the second soil layer. For comparison with the two versions of the SMAR model, we also calibrate the exponential filter approach (Wagner et al., 1999; Albergel et al., 2008) for the study site.

Different approaches exist to derive soil moisture from observed neutron signals. The standard approach following Desilets et al. (2010) is commonly used to derive soil moisture from CRNS but has been found insufficient, especially at observation sites with low soil moisture content. New approaches include the interdependence of the relationship between neutrons and soil moisture (Köhli et al., 2021) and report an improved estimation of surface soil moisture with CRNS.

The three depth-extrapolation approaches (SMAR, modified SMAR, and exponential filter) are therefore applied using different surface soil moisture time series, including single point-scale in situ sensor profiles, averages of the entire in situ sensor network, and CRNS-derived soil moisture from different neutron-to-soil moisture transfer functions in order to investigate the performance of the different approaches and if a better CRNS-derived surface soil moisture time series translates to better estimates of the depth-extrapolated soil moisture.

2 Material and methods

2.1 Study site

The study site is located in the TERENO-NE observatory (Heinrich et al., 2018) in the young Pleistocene landscape of north-eastern Germany (Fig. 1). The site hosts the CRNS sensor Serrahn (Bogena et al., 2022). The site has a mean annual temperature of 8.8 °C and mean annual precipitation of 591 mm yr⁻¹, as measured at the long-term weather station in Waren (in a distance of approximately 35 km), which is operated by the German Weather Service (station ID 5349; period 1981–2010) (DWD – German Weather Service, 2020a, b). It is situated on the southern ascent of a glacial terminal moraine formed during the Pomeranian Phase of the Weichselian glaciation in the Pleistocene (Börner, 2015). The dominating soil types in the vicinity of the sensor are Cambisols formed on aeolian sands, with depths of down to 450 cm, deposited during the Holocene (Rasche et al., 2023). Continuing downwards, these are followed by deposited glacial till of the terminal moraine, glacio-fluvial sediments, and glacial till originating from earlier glaciations with the latter forming the aquitard, the upper groundwater aquifer with water level depths ranging between 13 and 14 m below the surface (Rasche et al., 2023). A mixed forest dominated by European beech (Fagus sylvatica) and Scots pine (Pinus sylvestris) is the dominant land cover type. A clearing covered by grassy vegetation can be found nearby.

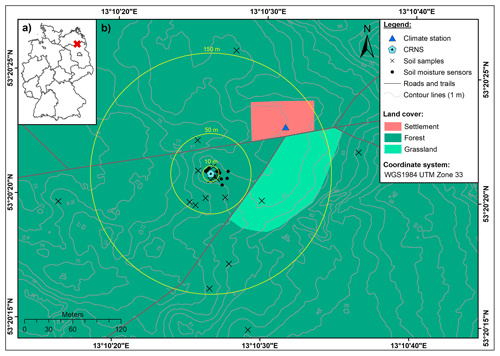
Figure 1 (a) The location of the study area within Germany and (b) the location of the CRNS observation site Serrahn (digital elevation model from LAIV-MV – State Agency for Interior Administration Mecklenburg-Western Pomerania, 2011; land cover from BKG – German Federal Agency for Cartography and Geodesy, 2018).

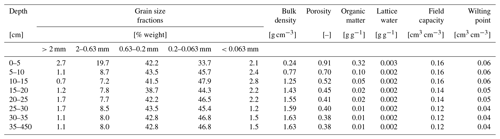
In order to calibrate the CRNS sensor, soil samples were taken at different distances around the instrument in February 2019 as shown in Fig. 1. Soil samples were taken in 5 cm depth increments from 0–35 cm using a split tube sampler containing sampling rings in order to derive soil moisture, soil physical characteristics, average grain size distributions, soil organic matter, and lattice water from laboratory analyses as shown in Table 1. Soil moisture and soil bulk density were determined by oven-drying at 105 °C for 12 h and gravimetric analyses of all individual soil samples. Subsequent loss-on-ignition analyses at 550 and 1000 °C that lasted 24 h were used to determine the amount of soil organic matter and lattice water from bulk samples per depth, assuming that no inorganic carbon is present in the acidic aeolian sands. Soil porosity was estimated based on the material density of quartz (2.65 g cm⁻³) and corrected for the amount of soil organic matter based on the density of cellulose (1.5 g cm⁻³).

In addition to the stationary CRNS instrument, the study site is equipped with a groundwater observation well, a weather station, and a network of in situ point-scale soil moisture sensor profiles (type SMT100; Truebner GmbH, Germany). A total of 59 in situ soil moisture sensors are deployed in depths down to 450 cm in depth with 12 sensors at 10 cm, 6 sensors at 20 cm, 8 sensors at 30 cm, 8 sensors at 50 cm, 6 sensors at 70 cm, 4 sensors at 130 cm, 7 sensors at 200 cm, and 4 sensors at 300 cm and 450 cm. The sensors are located at distances of up to 22 m from the CRNS instrument and continuously monitor the volumetric soil moisture content based on the manufacturer's calibration function.

Table 1 Soil physical characteristics at the CRNS site Serrahn obtained from laboratory analyses of soil samples (Rasche et al., 2023, modified). Below the maximum sampling depth of 35 cm and down to the maximum depth of the aeolian sand deposits, the soil physical parameters are assumed to have the same values as the layer between 30 and 35 cm. The soil moisture content at field capacity and wilting point were taken from tabulated values in Sponagel et al. (2005) according to the respective soil grain size class (medium-fine sand) and the soil bulk density of the individual layers.

2.2 Field-scale surface soil moisture derived with CRNS

Secondary neutrons are produced by primary cosmic rays interacting with matter in the atmosphere and in the ground. Depending on their energy level, secondary neutrons may be classified as fast (0.1–10 MeV), epithermal (> 0.25–100 keV), and thermal neutrons (<0.25 eV) (e.g. Köhli et al., 2015; Weimar et al., 2020). Cosmic-ray neutron sensing for soil moisture estimation relies on the number of neutrons in the epithermal energy range produced by nuclear evaporation in the atmosphere and ground (Köhli et al., 2015). Epithermal neutrons are sensitive to elastic scattering by collision with hydrogen and are further moderated to become thermal neutrons (<0.25 eV). Thus, the number of epithermal neutrons detected by the instrument is inversely correlated with the amount of hydrogen in the sensitive measurement footprint of the sensor.

Epithermal neutron counts detected by the instrument are influenced by the atmospheric pressure, the number of primary high-energy cosmic-ray neutrons entering the Earth's atmosphere from space (Zreda et al., 2012), and the variations in absolute air humidity (Rosolem et al., 2013) and need to be corrected for these influencing factors before soil moisture information can be derived. In this study, we use the correction procedure for air pressure and incoming primary cosmic-ray flux presented in Zreda et al. (2012). The correction factor for the shielding effect of the atmosphere can be calculated from local air pressure measurements, where the attenuation length, L, is set to 135.9 g cm⁻² for the study area (Heidbüchel et al., 2016). The correction factor for the incoming high-energy primary neutron flux was obtained from hourly pressure and efficiency-corrected primary neutron intensities (cps) of the Jungfraujoch neutron monitor (JUNG; https://www.nmdb.eu, last access: 15 September 2024). Furthermore, the neutron data were corrected for the influence of absolute air humidity introduced by Rosolem et al. (2013). The absolute humidity is calculated from relative humidity and temperature observations of the weather station at the observation site according to Rosolem et al. (2013). For all correction approaches, the time series averages of air pressure, incoming radiation and air humidity are used as the required reference values. Finally, a 25 h moving average filter is applied to the corrected neutron time series to reduce noise and uncertainty in the data (e.g. Schrön et al., 2018b).

$$\begin{array}{}\text{(1)}& \begin{array}{rl}{\mathit{\theta }}_{\text{Standard}}& =\left(\left(\stackrel{\mathrm{̃}}{a_{\mathrm{0}}}{\displaystyle \frac{\mathrm{1}-\frac{N_{\text{pih}}}{N_{\text{max}}}}{\stackrel{\mathrm{̃}}{a_{\mathrm{1}}}-\frac{N_{\text{pih}}}{N_{\text{max}}}}}\right)\times {\displaystyle \frac{{\mathit{\rho }}_{\text{soil}}}{{\mathit{\rho }}_{\text{water}}}}\right)\\ & -\left({\mathit{\theta }}_{\text{SOM}}+{\mathit{\theta }}_{\text{LW}}\right),\end{array}\end{array}$$

where

$$\begin{array}{}\text{(2)}& {\displaystyle }\stackrel{\mathrm{̃}}{a_{\mathrm{0}}}=-a_{\mathrm{2}},\text{(3)}& {\displaystyle }\stackrel{\mathrm{̃}}{a_{\mathrm{1}}}={\displaystyle \frac{a_{\mathrm{1}}{a}_{\mathrm{2}}}{a_{\mathrm{0}}+a_{\mathrm{1}}{a}_{\mathrm{2}}}},\text{(4)}& {\displaystyle }{N}_{\text{max}}=N_{\mathrm{0}}\cdot {\displaystyle \frac{a_{\mathrm{0}}+a_{\mathrm{1}}{a}_{\mathrm{2}}}{a_{\mathrm{2}}}}.\end{array}$$

Desilets et al. (2010) introduced a transfer function to convert neutron counts into soil moisture by calibration against reference measurements. Although other approaches exist (e.g. Franz et al., 2013; Köhli et al., 2021), the Desilets equation became the methodological standard and can be rewritten as Eqs. (1)–(4) (Köhli et al., 2021), with a₀=0.0808, a₁=0.372, and a₂=0.115, and N₀ is a local calibration parameter describing the neutron intensity above dry soil (Desilets et al., 2010). As observed epithermal neutron intensities are sensitive to any hydrogen present in the measurement footprint, the water equivalent of soil organic matter, θ_SOM, and the amount of lattice water, θ_LW, in cm³ cm⁻³ need to be subtracted in Eq. (1) to derive soil moisture. Additionally, ρ_soil describes the average soil bulk density in the measurement footprint (g cm⁻³) and ρ_water the density of water, assumed to be 1 g cm⁻³. In this neutron-to-soil moisture transfer function, the neutron intensity corrected for variations in air pressure, the incoming primary neutron flux, and absolute humidity, N_pih, is used. However, a more recent study by Köhli et al. (2021) suggests that the influence of absolute air humidity and soil moisture on the observed epithermal neutron signal is interdependent – that is, the shape of the neutron–soil moisture relationship changes with absolute humidity. The universal transport solution (UTS), Eqs. (5)–(6) (Köhli et al., 2021), accounts for the changing relationship between neutrons and soil moisture under different conditions of absolute humidity, h, in g m⁻³.

$$\begin{array}{}\text{(5)}& \begin{array}{rl}{N}_{\text{pi}}& =N_D\cdot ({\displaystyle \frac{p_{\mathrm{1}}+p_{\mathrm{2}}{\mathit{\theta }}_{\text{total}}}{p_{\mathrm{1}}+{\mathit{\theta }}_{\text{total}}}}\cdot \left(p_{\mathrm{3}}+p_{\mathrm{4}}h+p_{\mathrm{5}}{h}^{\mathrm{2}}\right)\\ & +e^{-p_{\mathrm{6}}{\mathit{\theta }}_{\text{total}}}\left(p_{\mathrm{7}}+p_{\mathrm{8}}h\right)),\end{array}\end{array}$$

where

$$\begin{array}{}\text{(6)}& {\mathit{\theta }}_{\text{total}}=\left({\mathit{\theta }}_{\text{UTS}}+{\mathit{\theta }}_{\text{SOM}}+{\mathit{\theta }}_{\text{LW}}\right)\cdot {\displaystyle \frac{\mathrm{1.43}\mathrm{g}{\mathrm{cm}}^{-\mathrm{3}}}{{\mathit{\rho }}_{\text{soil}}}}.\end{array}$$

The UTS is designed to describe the neutron intensity response caused by changes in total soil water content and absolute air humidity, and, therefore, the predicted neutron intensity represents the intensity corrected for variations in atmospheric pressure and incoming primary neutron flux, N_pi. Soil moisture can be derived from the UTS using numerical inversion or a lookup table approach, which is used in this study. In the lookup table approach, soil moisture values in the range from 0.0001 to 0.5 cm³ cm⁻³ in steps of 0.0001 cm³ cm⁻³ are used to predict the neutron intensity using the UTS for each time step. For each time step, the soil moisture value that produces the smallest absolute difference between the observed and predicted neutron intensity is then assigned as the CRNS-derived soil moisture value. Analogously to the standard transfer function, the UTS needs to be calibrated locally. The calibration parameter, N_D, may be interpreted as the average neutron intensity of the local neutron detector under the boundary conditions defined in the neutron transport simulations, which were used to subsequently derive the UTS. θ_total describes the total water content comprising the sum of all below-ground hydrogen pools – namely, the soil moisture content, θ_UTS, θ_SM, and θ_LW – which is then scaled by ratio of the soil bulk used in the neutron transport simulations to derive the UTS (1.43 g cm⁻³) and the local soil bulk density at the study site, ρ_soil (Köhli et al., 2021). Different sets of shape-giving parameters, p₁−p₁₀, are available for the UTS in Köhli et al. (2021) and originate from the different neutron transport models used and the fact whether a simple energy window threshold (thl) was used (parameter sets URANOS thl, MCNP thl) to evaluate the neutron transport simulations or a more complex detector response function was applied (parameter sets: URANOS drf, MCNP drf). The latter mimics the response of a real neutron detector and is therefore expected to provide more accurate results. In the scope of this study, we investigate which of the two transfer functions and which parameter set of the UTS perform best in estimating surface soil moisture.

The CRNS footprint diameter as well as the integration depth decrease with increasing soil water content. The radius ranges between 130 and 240 m and the integration depth ranges between 15 and 83 cm during wet and dry conditions, respectively (Köhli et al., 2015). In addition, further factors may influence the footprint dimensions, such as open water or topography (e.g. Köhli et al., 2015; Schattan et al., 2019; Mares et al., 2020). Consequently, reference measurements need to be depth–distance-weighted according to the sensitivity of the CRNS instrument in order to match field observations of reference measurements when calibrating the two different transfer functions and derive soil moisture information from observed neutron intensities. In this study, we adapt the weighting procedure proposed by Schrön et al. (2017), which takes the total water content, average bulk density, absolute air humidity, and vegetation height (set to 20 m) into account. Reference soil moisture information from the soil sampling campaign in February 2019 was weighted accordingly and used for calibrating both transfer functions. N₀ and N_D were iteratively calibrated. For N₀, the value producing the smallest RMSE between soil moisture from soil samples and the one predicted with Eqs. (1)–(4) was chosen. For N_D, soil moisture information derived from soil samples for the hours of the sampling campaign was used to predict neutron intensities with Eqs. (5)–(6). The N_D value that produced the smallest RMSE between predicted and observed neutron intensities was chosen. In a second step, the CRNS-derived soil moisture time series are compared to an analogously weighted average of all available in situ soil moisture sensors at 10, 20, and 30 cm depth. In order to assess the impact of the weighting procedure, the calibration is repeated using the arithmetic soil moisture average from soil samples and by comparing the CRNS-derived soil moisture time series to the arithmetic average soil moisture time series from in situ sensors.

2.3 Depth extrapolation of surface soil moisture time series

2.3.1 Modification of the SMAR model

To estimate depth-extrapolated soil moisture time series for a second, deeper soil layer from surface soil moisture time series, the SMAR model is used. Introduced by Manfreda et al. (2014), it allows for the physically based estimation of soil moisture in an adjacent second, lower soil layer from soil moisture information in a first, upper soil layer. SMAR is based on the relative saturation in the first and second layer – s₁ (–) and s₂ (–), respectively; the relative saturation at field capacity, s_c1 (–); and wilting point, s_w2 (–). In order to transform values from cm³ cm⁻³ to relative saturation, the respective variables are divided by the porosity of the individual layer, n₁ (cm³ cm⁻³) and n₂ (cm³ cm⁻³). After applying the SMAR model, the resulting relative saturation time series of the second layer, s₂ (–), is transformed back to volumetric soil moisture in cm³ cm⁻³ by way of multiplication with n₂ (cm³ cm⁻³), resulting in the depth-extrapolated soil moisture time series, θ_Layer 2. Soil moisture in layer 2 at time t is calculated by

$$\begin{array}{}\text{(7)}& \begin{array}{rl}{s}_{\text{2}}\left(t_i\right)& =s_{\text{w2}}+\left(s_{\text{2}}\left(t_{i-\mathrm{1}}\right)-s_{\text{w2}}\right)\cdot e^{-a\cdot \left(t_i-t_{i-\mathrm{1}}\right)}\\ & +\left(\mathrm{1}-s_{\text{w2}}\right)\cdot b\cdot y\left(t_i\right)\cdot \left(t_i-t_{i-\mathrm{1}}\right),\end{array}\end{array}$$

where a and b depend on the vertical extent of the first layer (Zr₁ in millimetres), which begins at the soil surface, and the vertical extent of the second layer (Zr₂ in millimetres). Zr₂ is the difference between the maximum depth of the second soil layer and Zr₁. The water loss term, V₂, (mm t⁻¹) comprises the bulk water losses from the second layer due to percolation and evapotranspiration per unit time:

$$\begin{array}{}\text{(8)}& {\displaystyle }a={\displaystyle \frac{V_{\mathrm{2}}}{\left(\mathrm{1}-s_{\text{w2}}\right)\cdot n_{\text{2}}\cdot {\mathrm{Zr}}_{\text{2}}}},\text{(9)}& {\displaystyle }b={\displaystyle \frac{n_{\mathrm{1}}\cdot {\mathrm{Zr}}_{\mathrm{1}}}{\left(\mathrm{1}-s_{\text{w2}}\right)\cdot n_{\mathrm{2}}\cdot {\mathrm{Zr}}_{\mathrm{2}}}}.\end{array}$$

The fraction of saturation of the first layer that instantaneously infiltrates into the second layer, y(t_i) (–), is described as follows (e.g. Manfreda et al., 2014; Patil and Ramsankaran, 2018):

$$\begin{array}{}\text{(10)}& y\left(t_i\right)=\left\{\begin{array}{ll}\left(s_{\mathrm{1}}\left(t_i\right)-s_{\text{c1}}\right),& s_{\mathrm{1}}\left(t_i\right)\ge s_{\text{c1}};\\ \mathrm{0},& s_{\text{1}}\left(t_i\right)<s_{\text{c1}}.\end{array}\right.\end{array}$$

The SMAR model can be applied using known soil physical and environmental variables. However, although the soil physical parameters may be estimated through pedotransfer functions, using tabulated values or global soil databases (e.g. SoilGrids 2.0; Poggio et al., 2021), the bulk water loss from the second layer, V₂, is more difficult to estimate. This hampers the use of SMAR without calibration against reference soil moisture information at the depth of interest – that is, in the deeper soil layer. To overcome this issue, we modified and extended the SMAR model (SMAR_modified) in order to estimate the V₂ based on simple physical and environmental soil variables and the surface soil moisture time series. A modification of the SMAR model with an extended definition of the water loss term, V₂, has been suggested by Faridani et al. (2017), leading to an improved performance compared to the original SMAR model. As any modification makes the SMAR model more complex and potentially less easy to apply, our aim was to keep the complexity added to the model low by only including three additional parameters. These are the relative saturations at field capacity in the second layer, s_c2 (–), and the cumulative root fraction to the maximum depth of the first and second layer – R₁ (–) and R₂ (–), respectively. The water loss term is then defined as the sum of evapotranspiration, ET₂ (mm t⁻¹), and percolation, P₂ (mm t⁻¹), from the second layer.

$$\begin{array}{}\text{(11)}& V_{\text{2}}={\mathrm{ET}}_{\text{2}}+P_{\text{2}}\end{array}$$

We adapt the suggestion of Manfreda et al. (2014) to make use of existing (surface) soil moisture time series to gain information about water loss from the soil by evapotranspiration at a study site. Here, we estimate the individual amount of evapotranspiration from the deeper layer, ET₂, for each time step based on the difference between the current and past value of relative saturation of the first layer by scaling the value to the dimension (i.e. extent) of the second layer and by considering the difference in cumulative root fraction between the two layers, assuming that root water uptake for ET is larger in the layer with more roots (Eq. 13). The required root fraction, R (–), for maximum depth d (cm) of the first and second layer is derived from the empirical equation (Eq. 12) for forest biomes presented in Jackson et al. (1996):

$$\begin{array}{}\text{(12)}& R=\mathrm{1}-{\mathrm{0.970}}^d.\end{array}$$

Using Eq. (13), ET₂ can only be estimated from the change in relative saturation in the first layer when (1) the relative saturation of the first layer, s₁, decreases; (2) no infiltration into the second layer occurs; and (3) the relative saturation of the second layer exceeds the relative saturation at wilting point. This means that both surface evaporation and transpiration losses are scaled from the first layer to the second layer. Although surface evaporation is hardly relevant for the second layer due to its missing connection with the surface, this is a reasonable yet simplified approach because surface evaporation is a comparatively small component of total evapotranspiration in forests, with transpiration dominating ET (e.g. X. Li et al., 2019; Paul-Limoges et al., 2020). The following applies:

$$\begin{array}{}\text{(13)}& {\mathrm{ET}}_{\mathrm{2}}\left(t_i\right)=\left\{\begin{array}{ll}\left(s_{\text{1}}\left(t_i-\mathrm{1}\right)-s_{\text{1}}\left(t_i\right)\right)\cdot n_{\mathrm{1}}& s_{\text{1}}\left(t_i-\mathrm{1}\right)\ge s_{\text{1}}\left(t_i\right),\\ \cdot {\mathrm{Zr}}_{\mathrm{1}}\cdot \frac{Z{r}_{\mathrm{2}}}{{\mathrm{Zr}}_{\mathrm{1}}}\cdot \frac{\left(R_{\mathrm{2}}-R_{\mathrm{1}}\right)}{R_{\mathrm{1}}},& y\left(t_i\right)>\mathrm{0},\\ & s_{\text{2}}\left(t_i-\mathrm{1}\right)\le s_{\text{w2}};\\ \mathrm{0},& \mathrm{otherwise}.\end{array}\right.\end{array}$$

The amount of percolation, P₂, from the second layer is estimated by analogy with the infiltration into this layer as an instantaneous water loss when the relative saturation exceeds field capacity, s_c2 (Eq. 14):

$$\begin{array}{}\text{(14)}& {\mathit{\text{P}}}_{\mathrm{2}}\left(t_i\right)=\left\{\begin{array}{ll}\left(s_{\text{2}}\left(t_i-\mathrm{1}\right)-s_{\text{c2}}\right),& s_{\text{2}}\left(t_i-\mathrm{1}\right)\ge s_{\text{c2}};\\ \mathrm{0},& s_{\text{2}}\left(t_i-\mathrm{1}\right)<s_{\text{c2}}.\end{array}\right.\end{array}$$

2.3.2 Comparison with the exponential filter method

To evaluate the performance of the original SMAR and the modified version, SMAR_modified, we also compared it to the exponential filter approach (soil water index, SWI; Wagner et al., 1999; Albergel et al., 2008). This approach is often applied to depth-extrapolated surface soil moisture time series (e.g. Zhang et al., 2017; Tian et al., 2020). It has also been used to depth-extrapolate surface soil moisture time series derived from CRNS (Peterson et al., 2016) as well as to evaluate the performance of the SMAR model (e.g. Manfreda et al., 2014). This exponential filter has a single calibration factor: the characteristic time length, T (in days). Although attempts have been made to investigate the controls of T and relate its variability to climatic variables, vegetation characteristics, and soil physical properties (e.g. Wang et al., 2017; Bouaziz et al., 2020), the characteristic time length, T, is commonly treated as a bulk calibration parameter which needs to be optimised against reference soil moisture information.

2.3.3 Application of depth-extrapolation approaches

We applied the SMAR model in its original form, with aggregated daily soil moisture data, by calibrating the V₂ water loss term as a constant value, while the remaining soil physical parameters were assigned according to Table 1. The modified version of the SMAR model (SMAR_modified) introduced in this study was applied with the same soil physical parameters but estimating daily V₂ based on Eqs. (11)–(14). Consequently, SMAR_modified was applied completely without calibration.

In order to apply and calibrate the exponential filter approach for comparison, the daily surface soil moisture time series was converted to relative saturation by dividing it by the porosity, n₁. The extrapolated second-layer time series of relative saturation based on the exponential filter is then converted back to soil moisture by multiplying it with the porosity of the second, deeper soil layer n₂. The same porosity values (Table 1) are used as for the application of SMAR and SMAR_modified.

The calibration and evaluation were performed against reference soil moisture time series in the deeper layer derived from in situ sensors of the soil moisture sensor network (SMN) that covers the entire study period. The reference soil moisture content of the second, deeper soil layer was calculated by weighting the individual sensor values according to their representative layer extent. For example, having soil moisture sensors installed at 30, 50, and 70 cm depth, the soil moisture content per time step observed at 50 cm is representative of the layer between 40 and 60 cm. The soil physical parameters assigned to the individual layers can be found in Table 1 and were weighted in the same way. The calibration is performed by minimising the root mean square error (RMSE) between the depth-extrapolated soil moisture time series and the entire reference soil moisture time series of the second soil layer.

The original SMAR with calibrated V₂, the modified SMAR model (SMAR_modified) with estimated V₂ (without calibration), and the exponential filter with calibrated T were applied to estimate a soil moisture time series in the second soil layer with a maximum depth below terrain surface of 70, 130, 200, 300, and 450 cm. The depth of the first soil layer was set to the median sensitive measurement depth of the CRNS method for the study period. We calculated the median CRNS measurement depth of the entire CRNS-derived soil moisture time series based on Schrön et al. (2017). According to Schrön et al. (2017), the sensitive measurement depth, D₈₆, is estimated using the calibrated CRNS-derived soil moisture time series for distances from 1 to 300 m around the instrument. Subsequent averaging allows for the estimation of the average measurement depth in the CRNS footprint for each time step of the time series. The time series median measurement depth, D₈₆, is then calculated for the soil moisture time series derived with the standard transfer function and the UTS. For both CRNS-derived soil moisture time series, the estimated median sensitive measurement depth is 20 cm.

The three depth-extrapolation approaches are applied in the following scenarios:

• Scenario Profile 1 and scenario Profile 2. Surface soil moisture is estimated separately from two individual profiles of in situ soil moisture sensors (average of the two sensors installed at 10 and 20 cm depth), and depth extrapolation is calibrated/evaluated against reference second-layer soil moisture calculated from the deeper sensors of the each individual sensor profile.

• Scenario SMN_arithmetic. Surface soil moisture is estimated with the arithmetic average of all in situ soil moisture sensors of the SMN (depth averages of sensors installed at 10 and 20 cm depth, with 12 and 6 sensors per depth), and depth extrapolation calibrated/evaluated against reference second-layer soil moisture calculated from the arithmetic depth averages of all in situ sensors of the SMN.

• Scenario SMN_weighted. Weighted average surface soil moisture is estimated after Schrön et al. (2017) from all in situ soil moisture sensors of the SMN at 10, 20, and 30 cm depth (26 in total), and depth extrapolation is calibrated/evaluated against reference second-layer soil moisture calculated from the arithmetic depth averages of all in situ sensors of the SMN.

• Scenario CRNS_{Revised standard}. Surface soil moisture time series from CRNS are based on the standard transfer function, and depth extrapolation is calibrated/evaluated against reference second-layer soil moisture calculated from the arithmetic depth averages of all in situ sensors of the SMN.

• Scenario CRNS_UTS. Surface soil moisture time series from CRNS are based on the UTS, and depth extrapolation is calibrated/evaluated against reference second-layer soil moisture calculated from the arithmetic depth averages of all in situ sensors of the SMN.

All calculations were performed in R statistical software (R Core Team, 2018, 2023) using the hydroGOF package (Zambrano-Bigiarini, 2017, 2020) for calculating goodness-of-fit measures which evaluate absolute values and time series dynamics – namely, the RMSE, the Kling–Gupta efficiency (KGE) (Gupta et al., 2009), the Pearson correlation coefficient, and the Nash–Sutcliffe efficiency.

3 Results and discussion

3.1 CRNS-derived surface soil moisture time series

The goodness of fit between the calibrated CRNS-based soil moisture time series and the time series derived from in situ point observations is shown for the two transfer functions (Table 2). When the different transfer functions are calibrated against an arithmetic average soil moisture from soil samples and compared to an arithmetic average of soil moisture time series at 10–30 cm depth, the Pearson correlation coefficient and the KGE are lower than when using a weighted average of soil moisture observations for calibration as proposed by Köhli et al. (2015) and Schrön et al. (2017). However, the RMSE is slightly higher for calibration against the weighted observations. This might be linked to differences between the laboratory measurements of soil moisture in the soil samples (which were used for calibration) and the continuous soil moisture data obtained from the in situ sensors. Overall, however, in view of the much better KGE and correlation values, the results underline the importance of the weighting procedures when calibrating the CRNS observations to derive soil moisture estimates or comparing them to observations from in situ soil moisture sensors.

Table 2 Goodness of fit between the CRNS-derived soil moisture time series and the arithmetic and weighted average soil moisture time series from the local in situ point-sale soil moisture sensors at 10–30 cm depth. The different neutron-to-soil moisture transfer functions are independently calibrated against soil moisture from soil samples taken in February 2019. The UTS transfer function can be used with different parameter sets, originating from different neutron transport models, which are based on either energy level threshold (thl) or a more realistic detector response functions (drf).

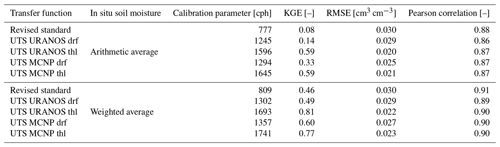
The goodness of fit of the CRNS-derived soil moisture time series that are based on the revised standard transfer function is always lower than for those that are derived with the UTS. All parameter sets, especially when the KGE is considered, show the improved soil moisture estimation with the UTS. However, the parameters sets of the UTS that mimic the varying sensitivity of a real neutron detector to neutrons of different energies (URANOS drf and MCNP drf) perform worse than those which rely on a simple energy range threshold (URANOS thl and MCNP thl). This counter-intuitive result has been previously described by Köhli et al. (2021) and could be related to the high sensitivity of the CRNS method to the soil moisture dynamics in the first few centimetres of the soil, where unfortunately no in situ sensors are installed (the uppermost sensors are installed at 10 cm depth). Therefore, the better performance of the energy threshold parameter sets of the UTS can be related to insufficient reference soil moisture information from the in situ sensor network. Generally, the UTS with the parameter sets that represent the response of a real neutron detector can be expected to provide more accurate results. Here, the UTS with parameter set MNCP drf reveals a higher statistical goodness of fit compared to the URANOS drf parameter set, which is in line with the findings presented in Köhli et al. (2021). The improved performance of the UTS with parameter set MNCP drf compared to the standard transfer function is shown in Fig. 2, revealing that the latter tends to overestimate soil moisture under the wet winter conditions and underestimate soil moisture under dry summer conditions.

Differently from the study of Köhli et al. (2021), which introduced the UTS, we apply UTS to derive soil moisture from neutron observations at a forest site. The UTS calibration parameter, N_D, represents the average count rate under boundary conditions of the neutron transport simulations conducted to derive the UTS. Therefore, N_D can be expected to be close to the average corrected neutron intensity observed at a study site with little or without vegetation or other above-ground hydrogen pools influencing the observed neutron intensity. At our study site, the calibrated N_D is much higher than the observed average corrected neutron intensity, N_pi (557 cph). This is probably caused by the influence of the forest vegetation on observed neutron intensities and the calibration parameter of the transfer function and has been similarly described for the standard transfer function by Baatz et al. (2015). As hydrogen stored in air humidity influences the functional relationship between neutron intensities and soil moisture, hydrogen stored in vegetation might have a similar effect. Therefore, a correction or inclusion approach for other above-ground hydrogen pools such as vegetation may yield an even better performance of the UTS and may be investigated in future studies.

Our analyses confirm the improved performance of the UTS compared to the standard transfer function. In order to test whether the improved performance in deriving surface soil moisture translates into a better estimation of soil moisture in deeper layers, we apply the SMAR model using the surface soil moisture time series based on both the revised standard transfer function and the UTS with the MCNP drf parameter set (Fig. 2).

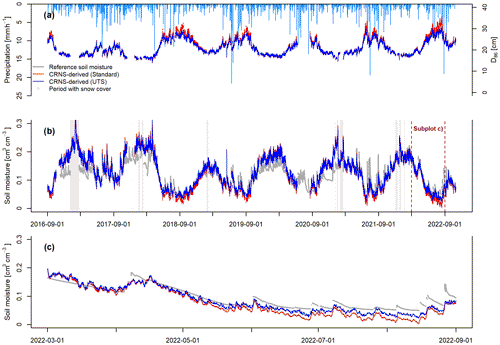
Figure 2 Soil moisture estimates with CRNS. (a) Estimated time-variable-sensitive measurement depth D₈₆ of the CRNS approach and precipitation time series (light-blue bars), (b) soil moisture time series derived with the revised standard transfer function and the UTS with parameter set MCNP drf, and (c) a period in 2022 illustrating the differences between the two CRNS-derived soil moisture time series.

3.2 Depth extrapolation of surface soil moisture time series

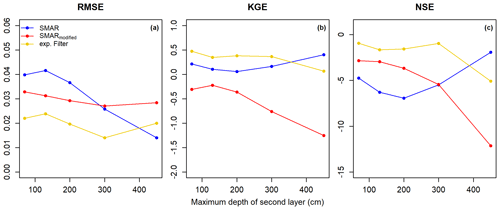
The performance of the different depth-extrapolation approaches – that is, based on the calibrated original SMAR (calibrated water loss only), the uncalibrated SMAR_modified (estimated water loss based on Eqs. 11–14), and the exponential filter approach (calibrated characteristic time length parameter) – for the different scenarios is listed in Tables A1–A3 and shown in Fig. 3. Figure 3 also includes a RMSE threshold of ≤0.06 cm³ cm⁻³, which has been used to evaluate the original SMAR performance in previous studies (Baldwin et al., 2019; Guo et al., 2023). In all scenarios and all depths, with the exception of SMAR_modified in the Profile 2 scenario, the RMSE of depth-extrapolated time series lies below this threshold, indicating that both SMAR models and the exponential filter approach result in acceptable soil moisture time series for the second soil layer down to 450 cm depth. However, goodness-of-fit indicators more sensitive to temporal dynamics, such as the KGE and the NSE, show negative values, indicating an insufficient simulation of the temporal dynamics of second-layer soil moisture time series compared to the reference. This can also be seen in Fig. 5, which shows the extrapolated soil moisture time series with the different approaches in a second layer, with a maximum depth of 130 cm. For example, comparing the scenarios of Profile 1 and Profile 2, the performance of the individual extrapolation approaches in terms of capturing the temporal soil moisture dynamics can differ strongly. These strong differences and largely unsatisfactory representation of soil moisture dynamics indicate that the RMSE threshold used in previous studies to evaluate the performance of depth-extrapolation approaches should be treated with caution. Regarding the exponential filter method, it should be noted that the maximum T value of 300 d defined in this study was reached during calibration in some scenarios, as displayed in Fig. 4.

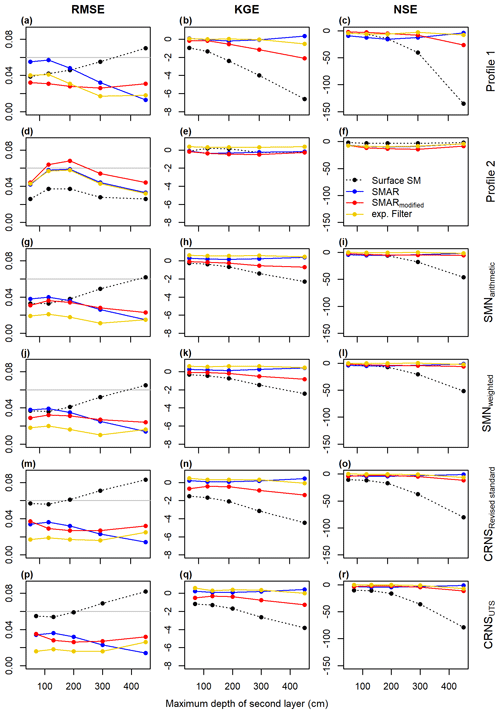
Figure 3 Goodness-of-fit parameters derived for the depth-extrapolation approaches in the individual scenarios depending on maximum second-layer depths. In addition to the three depth-extrapolation methods applied in this study, the comparison with the surface soil moisture time series is also shown. For the RMSE, a threshold value 0.06 cm³ cm⁻³ is indicated by the horizontal grey line.

Figure 3 also shows the goodness-of-fit parameters between surface soil moisture time series of the respective scenario and the reference soil moisture time series in the second soil layer in order to test if any of the depth extrapolations perform better than simply assuming that the soil moisture in the second layer is similar to the surface soil moisture time series. However, all depth-extrapolation approaches, including the uncalibrated SMAR_modified, show a better performance in most scenarios and especially in larger depths. This indicates that if no reference soil moisture time series for calibration in the depth of interest is available, the uncalibrated SMAR_modified provides better results than simply using the available surface soil moisture time series as a first estimate for the soil moisture time series in a second, deeper layer of interest. An exception to this finding is scenario Profile 2, where the NSE and RMSE of all depth-extrapolation approaches perform worse compared to using the surface soil moisture time series as the predicted time series in the second soil layer. Comparing the scenarios Profile 1 and Profile 2 in Fig. 5 shows large differences in the surface soil moisture time series between the two scenarios but a rather similar reference soil moisture time series in the second soil layer. This indicates small-scale heterogeneity of surface soil moisture within the SMN caused by, for example, heterogeneous infiltration, root water uptake, and preferential flow processes. Preferential flow in macropores, including bypass flow along roots (e.g. Nimmo, 2021), can result in highly conductive forest soils with infiltrating water being quickly transported from the surface to deeper layers and bypassing, for example, individual point-scale sensors. Heterogeneous evapotranspiration, interception (e.g. Schume et al., 2003), and root distribution patterns (e.g. Jost et al., 2012) add to the surface soil moisture heterogeneity in forests, which may explain the differing performance of all depth extrapolation approaches at different individual profiles of in situ soil moisture sensors. In larger depths with, for example, lower root densities, more similar soil moisture dynamics can be expected, which would explain the more similar soil moisture dynamics between the two individual sensor profiles. When assessing the results obtained from using the in situ sensor, it should also be noted that the use of the manufacturer's calibration function adds additional uncertainty to the results.

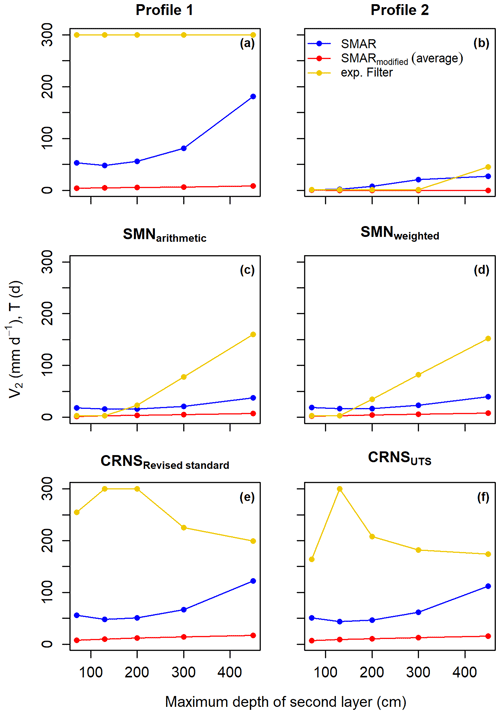
Figure 4 Optimum calibration parameters (minimum RMSE) derived for the different extrapolation approaches and depths in the individual scenarios. For SMAR_modified, the time series average of V₂ is shown.

Using averages of in situ soil moisture sensor networks therefore improves the performance of all depth-extrapolation approaches as shown in Fig. 6. Scenarios SMN_arithmetic and SMN_weighted as well as both CRNS scenarios generally show a higher goodness of fit for most depth-scaling approaches. This highlights the need for a representative estimation of surface soil moisture at complex study sites with strong small-scale heterogeneities in soil moisture and soil hydrological processes when depth-extrapolating surface soil moisture time series and underlining the potential of CRNS. The differences between SMN_arithmetic and SMN_weighted are rather small, indicating only a minor impact of using a weighted surface soil moisture time series and comparing it to a reference second-layer soil moisture time series calculated from arithmetic averages. Similarly, the difference between CRNS_{Revised standard} and CRNS_UTS is relatively small, with a slightly higher goodness of fit in scenario CRNS_UTS. However, as the differences are small, a clear conclusion that a better CRNS-derived surface soil moisture time series translates into a better depth-extrapolated time series cannot be drawn from the results of this study. This may also be linked to the differences in the CRNS-derived surface soil moisture time series being smaller than the uncertainties introduced by the different depth-extrapolation approaches.

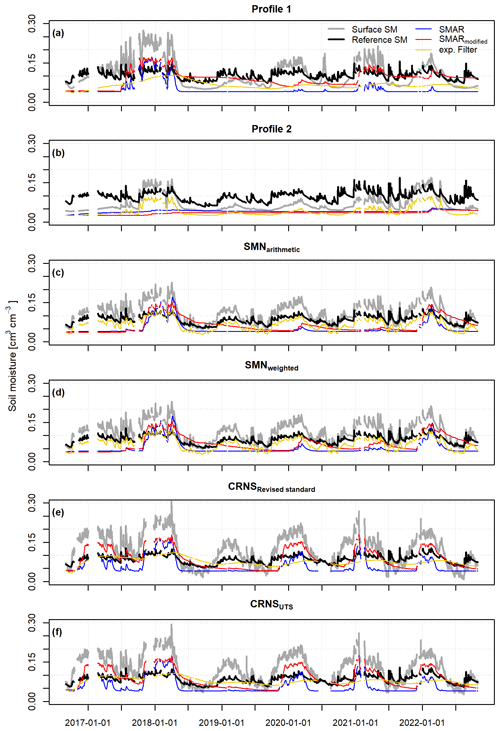
Figure 5 Daily depth-extrapolated soil moisture time series of the different scenarios and depth-extrapolation approaches for a depth of 130 cm. The respective surface soil moisture time series for the first soil layer (0–20 cm) and the reference soil moisture time series for the deeper, second soil layer (20–130 cm) are also shown.

In contrast, larger differences can be found between SMN scenarios (SMN_arithmetic and SMN_weighted) and CRNS scenarios (CRNS_{Revised standard} and CRNS_UTS), where the latter two often show lower goodness-of-fit parameters for the different extrapolation approaches as expressed by, for example, a lower KGE. This can be related to general differences between the surface soil moisture derived from the SMN and CRNS and could be related to the sensor locations of the SMN not being representative of the sensitive measurement footprint of CRNS. Also, the changing sensitive measurement depth of CRNS with soil moisture content may cause uncertainties when using a constant (median) sensitive measurement depth of 20 cm for the first soil layer in the depth-extrapolation approaches. Although this effect may be small, particularly on the daily time step, smoothing hourly CRNS data prior to estimating surface soil moisture and aggregating daily soil moisture estimates could contribute to the poorer performance of depth-extrapolated time series in the CRNS scenarios compared to the SMN scenarios.

Averaged over all tested scenarios, none of the three depth-extrapolation approaches properly represent the time series dynamics the our study site, as indicated by negative mean NSE values and KGE values being below 0.5 (Fig. 7). The highest average goodness of fit is obtained when applying the exponential filter approach calibrated against reference soil moisture measurements in the second soil layer of interest. The uncalibrated SMAR_modified shows average RMSE and NSE values lying largely between the exponential filter approach and the calibrated SMAR in its original form, indicating that the introduced SMAR_modified can compete with the (calibrated) original SMAR and can be applied without calibration to derive first estimates of soil moisture in a second, deeper layer.

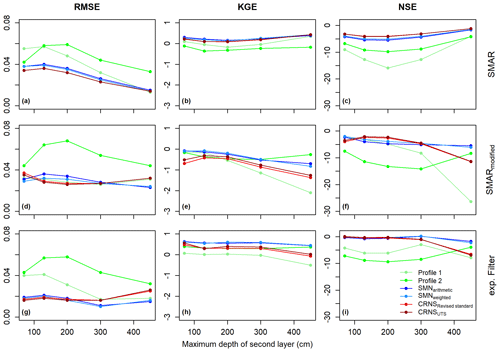
Figure 6 Goodness-of-fit parameters per depth-extrapolation approach and maximum second-layer depth for the individual scenarios.

Nevertheless, none of the three approaches produce satisfactory results in terms of soil moisture dynamics, which may be explained by the particular water flow dynamics at our study site located in a mixed forest with sandy soils. Complex preferential flow and infiltration processes are unlikely to be properly captured by any of the three depth-extrapolation approaches. This is especially true for SMAR and SMAR_modified as they allow for water movement only for soil moisture conditions above field capacity. In contrast, the exponential filter includes a constant dependence between the surface soil moisture dynamics of the first and of the deeper, second layer, which could be an explanation for its higher average performance at our study site, with expected highly conductive soils due to, for example, preferential flow processes. In addition, the decreasing number of reference in situ soil moisture sensors with increasing soil depth may lead to a lower representativeness of the reference soil moisture time series at greater depths, lowering comparability to the model results. However, with point sensors installed down to 450 cm, this study allows for the exploration of the potential of simple depth-extrapolation approaches for larger soil depths than commonly applied.

An important limitation of the present study for evaluating the standard and the introduced modified SMAR models is its application to a single observation site. Furthermore, other empirical approaches, such as regression models (e.g. Zhang et al., 2017) and cumulative distribution function matching (e.g. Gao et al., 2018), as well as other versions of the SMAR model (e.g. Faridani et al., 2017) would allow for an improved evaluation of the presented modification of the SMAR model and should be assessed in future studies at sites with a broader range of climatic conditions, vegetation covers, and soils.

Figure 7 Goodness-of-fit parameters of the three depth-extrapolation approaches averaged for all scenarios.

4 Conclusions

In the present study, we investigated the feasibility of depth-extrapolating surface soil moisture time series derived from CRNS to deeper soil layers without additional in situ soil moisture information for calibration. We furthermore evaluated the universal transport solution (UTS) for the estimation of field-scale soil moisture from CRNS neutron counts.

Being among the first who evaluate the UTS as a new transfer function to estimate field-scale surface soil moisture information from CRNS, we confirm its improved performance compared to the standard approach. The UTS accounts for the interdependence of soil moisture and air humidity on the observed neutron intensity, as it is most important for dry soil conditions. Although applied at a forested site with rather dry soils but with large amounts of above-ground hydrogen stored in the local biomass and influencing the neutron signal, CRNS-derived soil moisture estimates can be improved in contrast to established transfer functions. Thus, our results suggest that the UTS should be used for an improved estimation of surface soil moisture in future CRNS research and applications.

We modified SMAR for estimating soil moisture time series in a second, deeper layer in a way that it allows it to be applied without calibration against in situ sensors and with soil physical properties and the cumulative root fraction as a vegetation parameter only. Our analyses show that, on average, the uncalibrated SMAR_modified can compete with the original SMAR model down to a maximum depth of the second soil layer of 450 cm when the same soil physical properties are assigned and only the water loss term is calibrated. However, depending on the tested scenario, major temporal dynamics of the reference in situ soil moisture in the second soil layer are captured by neither the original nor the modified SMAR or the exponential filter approach. This is likely linked to the location of the study site: a forest with sandy soils, which results in soil moisture being influenced by processes such as preferential flow and root water uptake. These processes are difficult to simulate, especially with rather simple modeling approaches. On average, the calibrated exponential filter method performed best in predicting soil moisture in a deeper, second soil layer.

Although our study suggests that improved surface soil moisture estimates from CRNS do not translate to distinctly improved soil moisture estimates in greater depths at our study site, a more accurate estimation of CRNS-derived soil moisture information can be generally expected to lead to better results of the depth-extrapolation approaches.

Given the overall performance of the SMAR model at our single study site, further research and testing of the presented modified version of the SMAR model with and without calibration at sites with varying climatic conditions, vegetation cover, and soil properties are necessary and encouraged for future studies. Despite the overall unsatisfactory performance of the SMAR model with respect to accurately capturing soil moisture dynamics at our study site, it meets the defined RMSE benchmark of ≤0.06 cm³ cm⁻³, and the simple modification of the SMAR algorithm may serve as a valuable first estimate of soil moisture from a second, deeper soil layer when in situ reference soil moisture information for calibration are not available and the soil physical parameters can be estimated reasonably well.

In CRNS research, this modified SMAR approach opens up potential for roving CRNS, e.g. by mounting CRNS instruments on cars (e.g. Schrön et al., 2018a) or trains (e.g. Schrön et al., 2021; Altdorff et al., 2023) moving beyond the field-scale of stationary CRNS applications, thereby providing valuable information for landscape water balancing or hydrological catchment models on larger scales. Moreover, the modified SMAR approach introduced in this study is not limited to CRNS applications. It may also be used in estimating root-zone soil moisture at greater depths using satellite-derived surface soil moisture, where the original SMAR already proved useful (e.g. Baldwin et al., 2017, 2019; Gheybi et al., 2019).

Appendix A

Table A1 Statistical goodness of fit between the depth-extrapolated daily surface soil moisture time series and the reference soil moisture time series in the second layer extending from 20 to 70 and 130 cm for the different scenarios. The asterisk indicates that the maximum allowed characteristic time length value, T, was reached during calibration of the exponential filter method. Exp. stands for exponential.

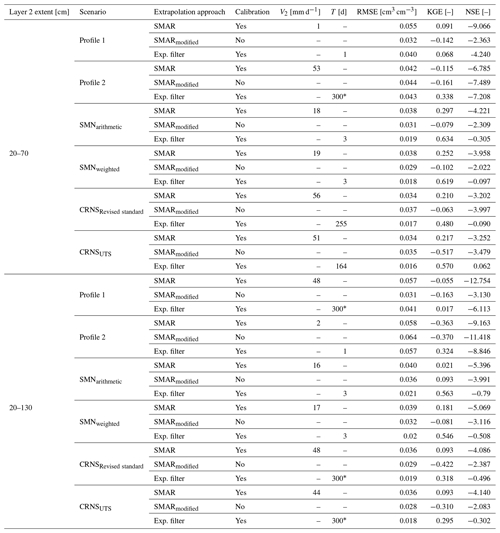
Table A2 Statistical goodness of fit between the depth-extrapolated daily surface soil moisture time series and the reference soil moisture time series in the second layer extending from 20 to 200 and 300 cm for the different scenarios. The asterisk indicates that the maximum allowed characteristic time length value, T, was reached during calibration of the exponential filter method. Exp. stands for exponential.

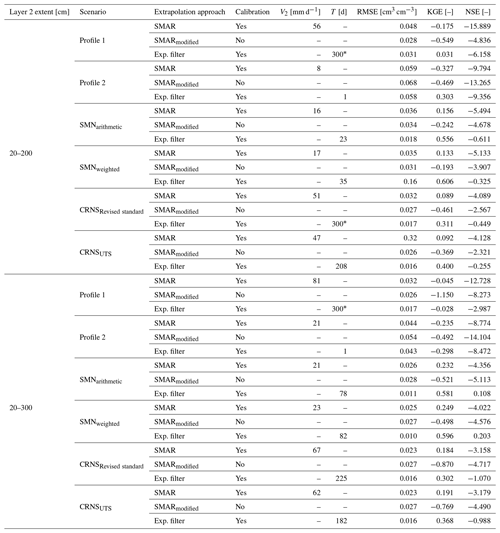
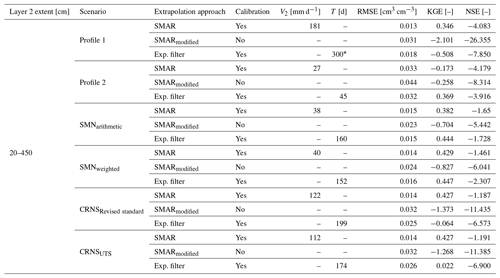
Table A3 Statistical goodness of fit between the depth-extrapolated daily surface soil moisture time series and the reference soil moisture time series in the second layer extending from 20 to 450 cm for the different scenarios. The asterisk indicates reaching the maximum allowed characteristic time length value, T, during calibration of the exponential filter method. Exp. stands for exponential.