Continental-scale controls on soil organic carbon across sub-Saharan Africa

Soil organic carbon (SOC) stabilization and destabilization has been studied intensively. Yet, the factors which control SOC content across scales remain unclear. Earlier studies demonstrated that soil texture and geochemistry strongly affect SOC content. However, those findings primarily rely on data from temperate regions where soil mineralogy, weathering status and climatic conditions generally differ from tropical and subtropical regions. We investigated soil properties and climate variables influencing SOC concentrations across sub-Saharan Africa. A total of 1601 samples were analyzed, collected from two depths (0–20 and 20–50 cm) from 17 countries as part of the Africa Soil Information Service project (AfSIS). The data set spans arid to humid climates and includes soils with a wide range of pH values, weathering status, soil texture, exchangeable cations, extractable metals and land cover types. The most important SOC predictors were identified by linear mixed-effects models, regression trees and random forest models. Our results indicate that geochemical properties, mainly oxalate-extractable metals (Al and Fe) and exchangeable Ca, are equally important compared to climatic variables (mean annual temperature and aridity index). Together, they explain approximately two-thirds of SOC variation across sub-Saharan Africa. Oxalate-extractable metals were most important in wet regions with acidic and highly weathered soils, whereas exchangeable Ca was more important in alkaline and less weathered soils in drier regions. In contrast, land cover and soil texture were not significant SOC predictors on this large scale. Our findings indicate that key factors controlling SOC across sub-Saharan Africa are broadly similar to those in temperate regions, despite differences in soil development history.

1 Introduction

Soil conservation and sustainable management are crucial to address some of the main challenges humanity is facing, such as climate change, food security, environmental degradation and loss of soil biodiversity. Assessing the state of soils and their potential responses to climate and land use change requires carefully designed sampling strategies combined with systematic analytical and statistical analyses across locations and scales (IPCC, 2019). One key component is soil organic carbon (SOC). Due to its variety of sources, transformations and stabilization mechanisms, SOC is chemically very complex and spatially heterogeneous. This complexity causes significant uncertainties in global climate models (Friedlingstein et al., 2014). It also complicates the extrapolation of SOC to a global scale using statistical relationships to build robust global SOC products, such as SoilGrids and the Harmonized World Soil Database (Tifafi et al., 2018). To improve our understanding of global C dynamics, it is important to better understand the factors that control SOC stabilization and destabilization in soils from regional to global scales (Blankinship et al., 2018; Heimann and Reichstein, 2008).

SOC-stabilizing drivers and processes have been intensively studied over the past several decades. Dokuchaev (1883) and Jenny (1941) shaped the understanding that soil properties are correlated with (independent) variables – the so-called soil-forming factors (Eq. 1) as follows:

$$\begin{array}{}\text{(1)}& s=f^{\prime }(\mathrm{cl},o,r,p,t),\end{array}$$

where s stands for any type of soil property, such as pH, carbon content, mineralogy, etc., and is determined by the function f^′ of the following soil-forming factors: cl – climate; o – organisms; r – topography; p – parent material; and t – time. This concept is still relevant and forms the basis for many experiments and research attempting to understand SOC storage. However, the importance of the individual factors of Eq. (1) at different spatiotemporal scales remains unclear (Doetterl et al., 2015; Rasmussen et al., 2018; Wiesmeier et al., 2019). This uncertainty hinders implementation of Eq. (1) in Earth system models, resulting in a gap between the theoretical understanding of SOM dynamics and our ability to improve terrestrial biogeochemical projections that rely on existing models (Blankinship et al., 2018; Rasmussen et al., 2018; Schmidt et al., 2011). Despite the long history of studying SOC stabilization (Greenland, 1965; Oades, 1988), there still is an increasing demand for data on SOC dynamics at landscape to global scales (Blankinship et al., 2018), especially from subtropical and tropical ecosystems.

SOC stabilization is commonly conceptualized as the competition between accessibility for microorganisms versus chemical associations with minerals (Oades, 1988; Schmidt et al., 2011). These processes are often only considered implicitly by models (Blankinship et al., 2018; Schmidt et al., 2011). Instead, models commonly rely on broader variables, such as clay content, which is used as a proxy for sorption and other organo-mineral interactions (Rasmussen et al., 2018; Schmidt et al., 2011). These more generic variables integrate a variety of stabilization processes which can be difficult to disentangle. They can differ in their relative importance and may not adequately capture soil mineralogy and chemistry across different ecosystems and climate zones. Hence, improving the predictive capacity of such models requires not only a better understanding of the factors that control SOC dynamics but also verification (or falsification) of those new findings in regions that are underrepresented in field studies and models.

For example, Rasmussen et al. (2018) found that exchangeable Ca was correlated with the quantity of SOC in water-limited soils, while Al_ox was a better predictor of SOC in wet, acidic soils. However, those findings may not be directly transferable to subtropical and tropical soils, since they differ greatly in climate, parent material and vegetation (Six et al., 2002b), which usually results in more weathered and older soils compared to those in temperate regions (Feller and Beare, 1997). This was illustrated recently in Quesada et al. (2020), where SOC variation in highly weathered forest soils from across the Amazon Basin was best explained by clay content, whereas the best explanatory variables for less-weathered soils were Al species, pH and litter quality. Feller and Beare (1997) also found that tropical soils, dominated by low-activity clays (i.e., 1:1 clays), show a strong relationship between SOC and clay and silt content. In addition, Barthès et al. (2008) found that sesquioxides (Al and Fe) play an important role in SOC stabilization for various tropical soils. However, the relationship for high-activity clays (i.e., 2:1 clays) is less clear, and contrasting trends between SOC and clay and silt content have been reported (Feller and Beare, 1997; Six et al., 2002a). In terms of SOC distribution across sub-Saharan Africa, Vågen et al. (2016) showed, by using a data set similar to the one in this paper, that SOC content was highest in equatorial and warm temperate climates where sand content, the sum of base concentrations and pH values were low. With regard to land cover, it has been shown for several sites across Africa that forests usually contained the highest amount of SOC, whereas the differences between cropland, grassland and shrubland were less distinct (Abegaz et al., 2016; Olorunfemi et al., 2020; Winowiecki et al., 2016a). Cropland cultivation decreased carbon content by 50 % compared to forested and semi-natural plots for sites in Tanzania, regardless of sand content and topographic position (Winowiecki et al., 2016b). Additionally, land degradation (i.e., erosion) resulted in decreased SOC concentrations in those ecosystems, independent of vegetation cover (Winowiecki et al., 2016a).

To address these diverging explanations of SOC variations at regional scales, we analyzed a comprehensive soil data set collected across the African continent using the Land Degradation Surveillance Framework (Vågen et al., 2010). This data set covers a wide range of climatic and mineralogical conditions – from very arid to humid regions, with different pH${}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ values, soil texture, weathering status, exchangeable cations and extractable metals – allowing us to test different parameters to explain the variation in SOC content in subtropical and tropical soils across sub-Saharan Africa for two distinctive depth layers (0–20 cm – topsoil; 20–50 cm – subsoil). Here, we use this continental-scale data set to address the following research questions:

1. Which soil properties and climate parameters best explain SOC content variation across sub-Saharan Africa?

   We explored the importance of soil texture, exchangeable Ca, oxalate-extractable Al and Fe, soil pH${}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$, mean annual temperature, aridity index (PET $/$ MAP), land cover and weathering status to explain the variation in SOC content on a continental scale. We expect that oxalate-extractable metals, soil texture and climate will be among the most important predictors of SOC concentration.

2. How do geochemical controls on SOC vary between environmentally distinct subregions?

   Due to the heterogeneity of climate and soil conditions across sub-Saharan Africa, we expect to see different geochemical controls explaining variations in SOC content between regions. For example, we expect exchangeable Ca will be most important in regions that are drier, with less weathered and alkaline soils, while oxalate-extractable Al and Fe will mainly be important in humid regions with highly weathered and acidic soils.

2 Methods

2.1 Study area and data collection

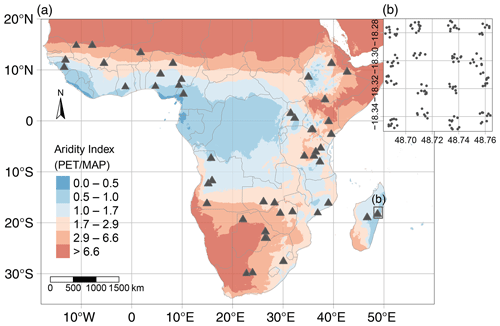
Soil data used in this study were collected during the AfSIS (Africa Soil Information Service) project. In total, 18 257 soil samples were taken from 60 sentinel sites and from two different depths (0–20 cm – topsoil; 20–50 cm – subsoil). Samples stem from 19 countries across sub-Saharan Africa and were collected between 2009 and 2012, following the well-established Land Degradation Surveillance Framework (Vågen et al., 2010). The 60 sentinel sites (each 100 km²) were stratified across sub-Saharan Africa according to Koeppen–Geiger zones (Vågen et al., 2016). Within each sentinel there were 10 plots of 1000 m² randomized within 16 spatially stratified 1 km² clusters (Fig. 1). This hierarchical sampling design allows process identification at a continental scale without losing the ability to understand and quantify local heterogeneity (Nave et al., 2021; Vågen et al., 2010). For more details about sampling design and field survey, see Towett et al. (2015), Vågen et al. (2013a) and Winowiecki et al. (2016a).

Our analyses built upon a subset of samples (11 % of the total; n=2002) which were originally selected as reference samples for laboratory measurements. These samples were used to calibrate mid-infrared spectroscopy models (Terhoeven-Urselmans et al., 2010) and to predict properties in the remaining 16 255 soil samples (Vågen et al., 2016; Winowiecki et al., 2017). The calibration subset was chosen to maximize the variation in the spectral data using the Kennard–Stone algorithm (Kennard and Stone, 1969). More information about this approach can be found in Terhoeven-Urselmans et al. (2010). This selection strategy results in unequally distributed samples across 51 of the 60 sentinel sites yet captures the variation in the original data set.

Figure 1 (a) Aridity index map and sampling scheme (n_total=1601). Gray triangles represent individual sentinel sites where sample clusters were collected. The top-right inset (b) shows the exact sampling points within one of the sentinel sites (Didy, Madagascar) as an example.

2.2 Sample and data processing

Soil material was air-dried and sieved to a particle size <2 mm in the Soil–Plant Spectroscopy Laboratory at the World Agroforestry Centre (ICRAF) in Nairobi, Kenya. All soil properties (except for soil texture, which was measured at ICRAF) were analyzed at Rothamsted Research in Harpenden, UK.

Data for soil organic carbon (SOC; weight percentage – wt %), pH${}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$, amorphous oxalate-extractable aluminum (Al_ox; wt %) and iron (Fe_ox; wt %, exchangeable calcium (Ca_ex; centimoles per kilogram), clay + fine silt content (<8 µm; percent), and total element concentrations (in wt %) of Al, Ca, K, and Na, were selected in order to cover a wide range of soil properties that have been identified to relate to SOC stabilization mechanisms (Oades, 1988; Rasmussen et al., 2018), while maximizing the number of samples and minimizing the correlation among variables included in our analysis.

SOC was calculated from the difference of total C and inorganic C. The latter was directly measured with a Primacs AIC100 analyzer (Skalar Analytical B.V., Breda, the Netherlands) by treating the sample with phosphoric acid and heating it to 135 ^∘C in a closed system. Inorganic C in the sample was converted to CO₂ and then measured by nondispersive infrared detection (NDIR). Total C was determined with the TruMac total N and C combustion analyzer (LECO Corporation, St. Joseph, Michigan, USA). Soil pH${}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ was performed in a 1:2.5 soil : water suspension. The extraction of Al and Fe with oxalic acid and ammonium oxalate solution was done by shaking the solution for 4 h at 25 ^∘C in the dark. Carbonate-rich samples were pretreated with ammonium acetate at pH 5.5 to remove any CaCO₃. Acid-oxalate extraction in particular dissolves short-range-order minerals such as ferrihydrite (Fe), allophane and imogolite (Al), as well as other amorphous and organic Fe and Al minerals (Parfitt and Childs, 1988). Hexamine-cobalt trichloride solution was used as an extractant to determine Ca_ex. Aqua regia acid digestion was applied for major and trace elements, including Al, Ca, K and Na. Although this method does not give absolute total contents, it does give results sufficiently close to accepted values for different soils (McGrath and Cunliffe, 1985). Samples were digested in tubes in time- and temperature-controlled heating blocks. All elements were measured with inductively coupled plasma optical emission spectrometry (ICP-OES; Optima 7300 DV, PerkinElmer Inc., Waltham, Massachusetts, USA). Particle size distribution was measured using a laser diffraction particle size analyzer (LDPSA) model LA-950 (HORIBA, Ltd., Kyoto, Japan). Each sample was shaken for 4 min in a 1 % sodium hexametaphosphate (calgon) solution with ultrasonic energy before measuring to disperse aggregates. We used 8 µm as cut-off to capture all clay + fine silt particles. Results were comparable to <20 µm (see Appendix Fig. A1), but <8 µm was selected because it is more relevant to our interest in studying the influence of smaller particles with large surface area on SOC concentration. In addition, particles <8 µm resulted in a reproducible fraction across soil types, unlike using only clay particles <2 µm (Fig. A1). Aluminum, Ca, K and Na concentrations were used to calculate the chemical index of alteration (CIA) after Nesbit and Young (1982), using the following equation:

$$\begin{array}{}\text{(2)}& \mathrm{CIA}={\mathrm{Al}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{3}}/\left({\mathrm{Al}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{3}}+\mathrm{CaO}+{\mathrm{K}}_{\mathrm{2}}\mathrm{O}+{\mathrm{Na}}_{\mathrm{2}}\mathrm{O}\right)\times \mathrm{100},\end{array}$$

where CaO is the amount incorporated in the silicate fraction. Correction is necessary for samples that contain carbonates and apatite (Nesbit and Young, 1982). We adopted an approach introduced by McLennan (1993), which assumes that Ca is typically lost more rapidly than Na during weathering. If a soil sample contained inorganic C (C_total–C_org; used as a proxy for carbonates and apatite) and the CaO content was greater than that of Na₂O in the same sample (n=476), then the CaO concentration was set to that of Na₂O from the same sample (Malick and Ishiga, 2016). After applying the correction, no obvious correlation remained between CIA and inorganic C (Fig. A3). The index increases (i.e., more highly weathered soil) with the loss of Ca²⁺, K⁺ and Na⁺.

Samples were removed that contained missing or negative values for one or more of the abovementioned parameters. In addition, a single sample with extraordinarily high SOC content (>22 wt %) was excluded. This resulted in a total of 1601 soil samples (out of the original 2002 samples) at 45 sentinel sites across 17 countries. Note that due to the sample selection, not all profiles had data from both topsoil and subsoil layers (Table B1).

The remaining soil samples (n=1601) were paired (based on longitude and latitude at the profile level) with mean annual temperature (MAT; degrees Celsius) and mean annual precipitation (MAP; millimeters) from the WorldClim data set at 30 arcsec resolution (Fick and Hijmans, 2017). Potential annual evapotranspiration (PET; millimeters) was added from Trabucco and Zomer (2019), who calculated it after the Penman–Monteith method, based on the WorldClim data. Mean annual precipitation and PET were used to calculate an annual aridity index, defined as PET $/$ MAP (Budyko, 1974). Values >1 indicate water-limited (dry) regions and ratios <1 point to energy-limited (wet) regions. For the monthly aridity index, we used monthly climate data at the same spatial resolution and from the same data sources.

Land cover data was used from the collected field data. The land cover groups were reclassified into the following four major groups: (a) cropland (including all cultivated plots), (b) forest, (c) grassland and (d) other (including mainly woodland, shrubland and bushland but also samples classified as other). A total of 10 missing values were gap-filled from a prototype high-resolution Africa land cover map at 20 m resolution based on 1 year of Sentinel-2A observations from December 2015 to December 2016 (http://2016africalandcover20m.esrin.esa.int/, last access: 9 June 2020).

Due to the lack of precise data products for lithology and soil types in sub-Saharan Africa, we did not include these variables in our analyses. Soils at AfSIS sites (Fig. 1) developed mainly from two parent material types, (i) metamorphic and (ii) volcanic rocks (Hartmann and Moosdorf, 2012; Jones et al., 2013; Schlüter, 2008), likely modified throughout the Quaternary. (i) Metamorphic rocks are most commonly found in West Africa, southern Africa and Madagascar. These regions are characterized by old cratons, except for Madagascar, which is influenced by Mesozoic volcanism (Schlüter, 2008). Most of these soils are classified as Ferralsols (World Reference Base, WRB, soil classification system; Jones et al., 2013). Related AfSIS soils from those regions are usually highly weathered with low pH${}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ values. In contrast, soils derived from (ii) volcanic rocks are mainly found in the East African Rift System. They are usually younger and less weathered (Buringh, 1970). Beyond the influence of volcanic rocks, Ca²⁺ rich soils are frequent in East Africa.

2.3 Statistical analyses

We used three different statistical approaches, including linear mixed-effects models, regression trees and random forests, to determine geochemical and climatic parameters that best explain SOC variation across sub-Saharan Africa. In brief, we used linear mixed-effects models to handle the hierarchal sampling design of the AfSIS data set, whereas regression trees and random forests enabled us to account for nonlinearities within the data. More precisely, we used regression trees as a qualitative tool to explore and understand the structure of the data, whereas random forests offered more generalizable models. All statistical analyses were performed within the R computing environment (version 4.0.0; R Core Team, 2020). The R Markdown file in the Supplement provides the code to reproduce all our analyses.

Linear mixed-effects modeling was performed using the nlme R package (Pinheiro et al., 2020) to account for the nested sampling scheme (clusters within sites and two sampling depths within one profile). This allows the intercept of the regression to vary for each site, for each cluster within the same site and for each sample within the same profile (Harrison et al., 2018). The variance inflation factor was used to check for multi-collinearity among predictor variables with a threshold of <3.0 (Zuur et al., 2010). To meet linear mixed-effects model assumptions and to standardize variation among variables, all continuous parameters were transformed to a normal distribution using Box–Cox transformation, followed by standardization to a mean of 0 and standard deviation of 1 by using the R package bestNormalize (Peterson and Cavanaugh, 2019). The relationship between SOC and the predictors of the original data may not be linear.

To answer our first research question, i.e., which soil properties and climate parameters best explain SOC content, we started from a constant null model with siteID/clusterID/plotID as random effects and then extended the model in a step-wise manner by fitting the following sequence of fixed effects: MAT, PET $/$ MAP, depth, land cover, clay + fine silt, pH${}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$, CIA, M_ox (Al_ox + $\mathrm{1}/\mathrm{2}$ Fe_ox), Ca_ex, and pH${}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ × M_ox. The order and selection of fixed effects was predefined based on a priori knowledge from a larger set of variables (Burnham and Anderson, 2002), starting with large-scale climate variables and ending with fine-scale physiochemical soil properties. The oxalate-extractable metals Al_ox and Fe_ox were summed to M_ox (Al_ox + $\mathrm{1}/\mathrm{2}$ Fe_ox) to normalize the atomic mass difference between Al and Fe (Wagai et al., 2020) and to account for their similar behavior over their concentration range (Fig. 5b). The maximum likelihood method and likelihood ratio tests (L. ratio) were applied to evaluate model performance and the statistical significance of the added fixed effects (Tables B4–B9). The variation explained by each fixed effect was obtained by calculating the marginal R² (excluding the variation explained by the random effects siteID/clusterID/plotID) for each model and subtracting the R² from the previous fitted model using the function r.squaredGLMM from the MuMIn R package (Barton, 2020; Nakagawa and Schielzeth, 2013). To identify how much SOC variation is explained by climate and geochemistry only (Legendre and Legendre, 2012), we built one model with climate parameters (MAT and PET $/$ MAP) only and one model with geochemistry variables (clay + fine silt, pH${}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$, CIA, M_ox, Ca_ex and pH${}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ × M_ox) only. In addition, we analyzed the two sampling depths (0–20 and 30–50 cm) separately to determine whether the same factors are important for topsoil versus the deeper soil layer (Table 1). For this model, we did not include plotID as a random effect since each profile only contained one sample in each depth model.

For the second research question, i.e., how geochemical controls on SOC content vary between environmentally distinct subregions, we grouped the data based on (a) pH${}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$, (b) wetness, (c) weathering and (d) land cover (Table 1). Soil pH${}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ and weathering data were grouped with the number of categories chosen to maximize and equalize the number of samples in each category and to correspond with common pH${}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ and weathering groups (Nesbit and Young, 1982). In order to take seasonality of the sites into account separately, the data were divided into three categories based on the number of wet months (i.e., months with P $/$ PET > 1). Land cover was grouped based on the four predefined categories. For each category within each subgroup, we built a linear mixed-effects model, as previously described, yet only included the geochemical properties (clay + fine silt, pH${}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$, CIA, M_ox, Ca_ex and pH${}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ × M_ox) as fixed effects, since we intended to test if the importance of these predictors changed between environmentally distinct subregions (Table 1). When CIA or pH${}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ were used to create the categories, they were not included as a fixed effect in the corresponding submodels.

Table 1 Grouping variables, subgroups, number of samples and fixed effects used for the linear mixed-effects models.

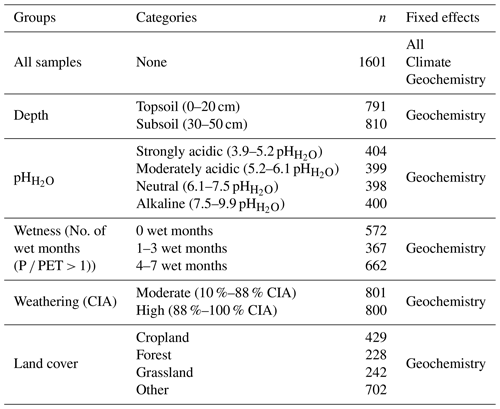
P – monthly precipitation (millimeters); PET – monthly potential evapotranspiration (millimeters); CIA – chemical index of alteration (percent); fixed effects – all (i.e., mean annual precipitation (MAT), aridity index (PET $/$ MAP), depth, land cover, clay + fine silt, pH${}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$, CIA, oxalate-extractable metals (M_ox), exchangeable Ca (Ca_ex) and pH${}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ × M_ox); climate (MAT, PET $/$ MAP); and geochemistry (i.e., clay + fine silt, pH${}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$, CIA, M_ox, Ca_ex and pH${}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ × M_ox).

Regression tree (R packages rpart and rpart.plot; Milborrow, 2019; Therneau and Atkinson, 2019) and random forest analyses (R package ranger; Wright and Ziegler, 2017) were conducted to identify nonlinear relationships between SOC and any explanatory variable. This also enabled the identification of pedogenic thresholds within the data. Each analysis was conducted with the same explanatory variables as for the linear mixed-effects models. However, no data transformation was needed due to the nonlinearity of the models.

Regression tree analysis was applied to obtain an easily interpretable and nonlinear model for the entire data set and for both depth layers (topsoil vs. subsoil) that best describes the existing data (Breiman et al., 1984). Since regression trees are known to easily overfit data, we used a grid search to prune the model (Boehmke and Greenwell, 2020), according to the minimum number of data points required to attempt a split and the maximum number of internal nodes between the root node and terminal nodes, in order to minimize the cross-validation error (Breiman et al., 1984). The overall performance of the regression tree analysis was tested using a five-fold spatial cross-validation (R package mlr; Bischl et al., 2016). Spatial partitioning was used to split the data into five disjoint subsets, using the coordinates from each sample and repeating the partitioning 100 times (Fig. A4). This results in a bias-reduced assessment of model performance (Brenning, 2012; Lovelace et al., 2019). Absolute values at the bottom of each node indicate the predicted SOC content (wt %) and the percentage corresponds to the relative number of samples in this node (Fig. A6).

Random forest was used to build more generalized models since it is an ensemble of multiple decorrelated trees. Tuning of the model hyperparameters was done based on spatial tuning (R package mlr; Bischl et al., 2016; Lovelace et al., 2019). These hyperparameters included the number of predictors used at each split, the minimum number of observations in a terminal node and the fraction of samples used in each tree (Probst et al., 2019). The best hyperparameter combination search was done for the complete data set via a five-fold spatial cross-validation with one repetition. In each of these five spatial partitions, we ran 50 models to find the optimal hyperparameter combination (Lovelace et al., 2019).

Partial dependence plots were used to further explore the relationship between the predicted SOC content and the explanatory variables of the tuned random forest models (R package pdp; Greenwell, 2017). These plots were used to investigate the marginal effect of individual explanatory variables (such as Al_ox, Ca_ex, etc.) on the predicted SOC content (Friedman, 2001). This allowed us to identify thresholds within the data and provided an indication of how important each explanatory variable was for the prediction of SOC concentration across specific value ranges.

3 Results

3.1 Data distribution across sub-Saharan Africa

All soil and climate variables spanned at least 1 order of magnitude (except MAT and PET), demonstrating the diversity of this continent-wide data set. Based on skewness, kurtosis, histograms and Shapiro–Wilk tests (data not shown for the latter two), no variable was normally distributed (Table 2).

Table 2 Summary statistics of all numerical soil and climate variables for the entire data set (n_total=1601; n_Topsoil=791; n_Subsoil=810).

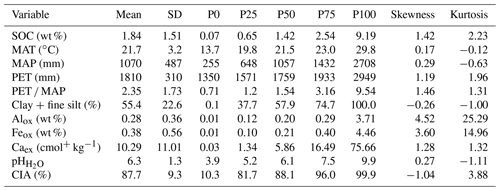
SD – standard deviation; P – percentile; SOC – soil organic carbon; MAT – mean annual temperature; MAP – mean annual precipitation; PET – potential evapotranspiration; Al_ox – oxalate-extractable Al; Fe_ox – oxalate-extractable Fe; Ca_ex – exchangeable Ca; CIA – chemical index of alteration.

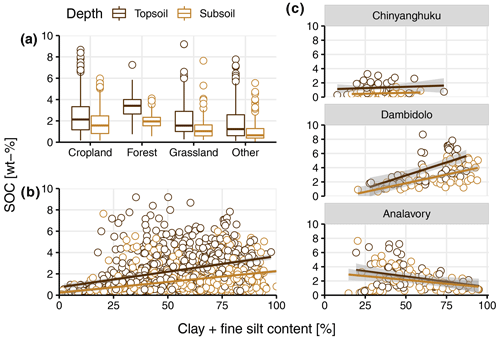
Figure 2 (a) Soil organic carbon (SOC) content (wt %) for the different land covers, i.e., cropland, forest, grassland and other (bushland, shrubland and woodland) by depth (0–20 cm – topsoil; 20–50 cm – subsoil). (b) SOC (wt %) and clay + fine silt content (<8 µm) (percent) by depth. (c) SOC (wt %) and clay + fine silt content (<8 µm) (percent) by depth for three example sites that show contrasting trends. The gray area around fitted linear regressions (y–x; for illustration only) in (b) and (c) shows the 95 % confidence interval. For the relationship between SOC (wt %) and clay + fine silt content (<8 µm) (percent) for all individual sites (see Fig. A5).

In total, 429 samples were classified as cropland, 228 as forest, 242 as grassland and 702 as other land covers, including mainly shrubland, bushland and woodland. The SOC content decreased among those groups in the following sequence: forest (2.69 ± 1.15 wt %) > cropland (2.21 ± 1.68 wt %) > grassland (1.77 ± 1.55 wt %) > other (1.35 ± 1.28 wt %; Fig. 2a). Clay + fine silt content and SOC showed a positive relationship across the entire data set yet with a large spread (Fig. 2b). However, individual sites showed contrasting correlations between SOC and clay + fine silt content, including none, positive and negative values (Figs. 2c; see A5 for all individual sites).

3.2 Predictors of soil organic carbon

Linear mixed-effects modeling

The full linear-mixed effects model for the entire data set had a marginal R² of 0.72. The two climate parameters (MAT and PET $/$ MAP), depth, M_ox and Ca_ex were the most important predictors of SOC content, based on their marginal R². Land cover, clay + fine silt, pH${}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$, CIA and pH${}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ × M_ox contributed either little or nothing to the overall explanatory power of the model. Clay + fine silt content, M_ox and Ca_ex were positively correlated with SOC, whereas all other fixed effects showed negative relationships with SOC concentration. The negative coefficient for depth indicates that the SOC content in the subsoil layers is, on average, lower as compared with the topsoil samples (Fig. 3a).

The marginal R² for the geochemistry model was 0.46, which is almost the same as for the climate model (R²=0.48). For the geochemistry model, the contribution of M_ox and Ca_ex to explain SOC content was much higher than in the full model (Fig. 3a). Based on variation partitioning, 27 % of the explained variation is shared between the geochemistry model and the climate model, whereas the variation explained by the geochemical or climate variables alone is 19 % and 21 %, respectively (Fig. 3b).

Differences between the predictors were negligible for the two depth models (topsoil vs. subsoil). However, the explained variation by clay + fine silt was larger in the subsoil layers compared with the topsoil layers. For Ca_ex, the opposite was true (Fig. 4a).

Within the pH${}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ submodels, M_ox was most important in the strongly acidic model. The opposite was observed for Ca_ex (Fig. 4b), which corresponds to higher concentrations of Ca_ex in neutral and alkaline soils compared with moderately and strongly acidic soils. However, Ca_ex was also found to have a positive relationship with SOC in acidic soils (Fig. 5; Table B2). The direction of the correlation between clay + fine silt and SOC concentration was not consistent across the four pH groups, in contrast to the other fixed effects (Table B2). The alkaline submodel had the lowest marginal R² of all pH${}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ submodels, which suggests that important predictors were missing (Fig. 4b).

Table 3 Marginal R² for each predictor based on sequential fitting of the linear mixed-effects models of all samples (n_Total=1601) for the full, geochemistry-only and climate-only models. The sign in parentheses refers to the correlation between the predictors and soil organic carbon. Bold values have a p value < 0.05 based on likelihood ratio tests.

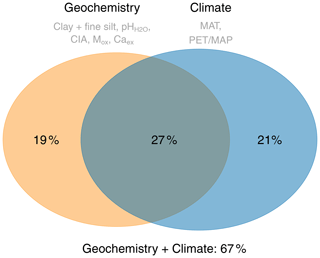
Figure 3 Venn diagram illustrating the independent and shared variation explained by the geochemistry-only and the climate-only linear mixed-effects models.

Grouping by the number of wet months (wetness) showed that M_ox explained most of the variation in wet regions, whereas Ca_ex was most important in drier regions (Fig. 4c). This corresponds to the overall distribution of M_ox and Ca_ex across MAP and pH${}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ (Fig. 5b). The chemical index of alteration (CIA) explained most of the variation in the intermediate wet regions (Fig. 4c).

The high weathering model was dominated by M_ox, whereas the importance of M_ox and Ca_ex in the moderate weathering model was similar. The other fixed effects did not explain much of the variation in the two weathering models (Fig. 4d).

Within the land cover models, the cropland and grassland models had the highest marginal R² and were both dominated by M_ox. The variation explained by Ca_ex was smallest for the forest model, whereas it did not change much for the other three models (Fig. 4e).

In summary, in the linear mixed-effects models, M_ox was more important in wetter regions and acidic and highly weathered soils, whereas Ca_ex was more important in drier regions and alkaline and less weathered soils. The other fixed effects usually did not explain much of the SOC variation.

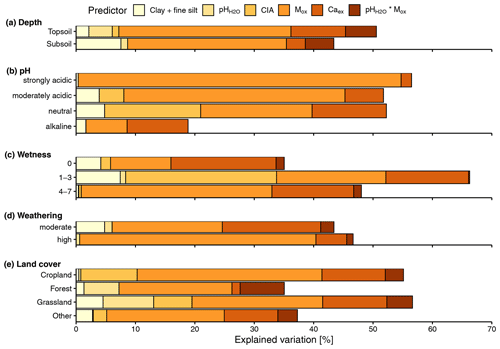
Figure 4 Explained variation (based on marginal R²) for each fixed effect, based on sequential fitting of the linear mixed-effects models grouped by (a) depth (0–20 cm – topsoil; 20–50 cm – subsoil), (b) pH classes (3.9–5.2 pH – strongly acidic; 5.2–6.1 – moderately acidic; 6.1–7.5 – neutral; 7.5–9.9 – alkaline), (c) wetness (no. of wet months; P $/$ PET > 0; 0, 1–3, 4–7), (d) weathering (CIA – chemical index of alteration; 10 %–88 % CIA – moderate; 88 %–100 % – high) and (d) land cover.

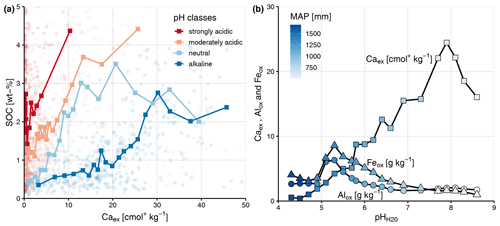
Figure 5 (a) Soil organic carbon (SOC) (wt %) and exchangeable Ca (Ca_ex; centimoles per kilogram) content colored by pH classes (3.9–5.2 pH – strongly acidic; 5.2–6.1 – moderately acidic; 6.1–7.5 – neutral; 7.5–9.9 – alkaline) with binned averages (bold squares; n=20). Note that the x axis is truncated for improved visualization, which removes three data points (Ca_ex=53.91, 54.58 and 75.66 cmol⁺ kg⁻¹). (b) Al_ox, Fe_ox (grams per kilogram; which were combined to M_ox, i.e., Al_ox+ $\mathrm{1}/\mathrm{2}$ Fe_ox, for the linear mixed effects models) and Ca_ex (centimoles per kilogram) averaged content (n=20) across pH${}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ and mean annual precipitation (MAP; millimeters).

3.3 Regression tree and random forest

The root mean squared error (RMSE) for the topsoil regression tree was 1.47 wt % (range = 0.80 wt %–3.11 wt %) and for the subsoil regression tree was 0.67 wt % (range = 0.44 wt %–2.26 wt %); the relative RMSEs were 0.65 % and 0.48 %, respectively. In the topsoil regression tree (Fig. A6a) Fe_ox, MAT and PET $/$ MAP were the most important predictors to split and explain the variation in SOC concentration. About 23 % of the SOC data could be explained by Fe_ox and MAT alone. In general, higher Fe_ox, Al_ox and Ca_ex values resulted in higher SOC content. This was equally true for the subsoil tree (Fig. A6b). While much of the SOC variation was explained by climate parameters in topsoils, the subsoil regression tree was more dominated by geochemical variables, namely Fe_ox and Al_ox. About 40 % of the subsoil SOC variation could be explained by Fe_ox only. In both trees, clay + fine silt content and land cover poorly predicted SOC.

In summary, topsoil and subsoil regression trees contained the same predictors, but climate variables played a larger role in the topsoil regression tree, and geochemistry had a larger influence in the subsoil regression tree. Overall, the results showed that the explanatory variables did not differ much between the depth intervals (topsoil vs. subsoil), while their magnitude did.

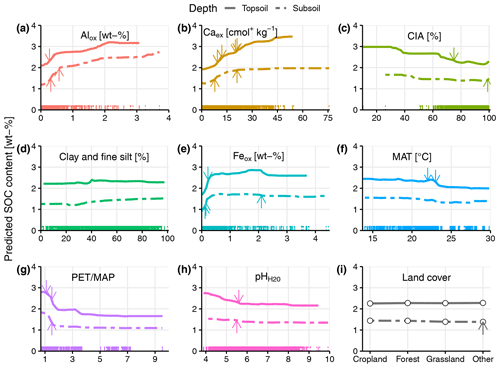
Figure 6 Partial dependence plot for each explanatory variable of the random forest models (topsoil and subsoil). The x axes always correspond to the range of the explanatory variable. Arrows indicate splitting points in the regression tree (Fig. A6). Each colored tick mark along the x axes represents one sample.

The random forest models had a RMSE of 1.31 wt % and a R² of 0.70 for the topsoil samples, and for the subsoil samples, they had a RMSE of 0.87 wt % and a R² of 0.72. Based on the partial dependence plots (Fig. 6), Al_ox and Ca_ex were important in predicting SOC over the entire range of each variable (Fig. 6a and b). However, in subsoils, the predictive power of Ca_ex was reduced (Fig. 6b). We observed a decrease in the predicted SOC with increasing soil weathering status (CIA). However, due to the low number of samples with CIA values below 60 %, the relationship should be interpreted with caution in this range (Fig. 6c). Clay + fine silt content had almost no effect on SOC, with only a weak positive trend in subsoil samples (Fig. 6d). The relationship between Fe_ox concentration and predicted SOC content varied with Fe_ox concentration. At low concentrations (<0.25 wt %), there was a strong positive relationship between predicted SOC content and Fe_ox. For higher concentrations, the predicted SOC content was relatively constant (Fig. 6e). MAT correlated negatively over the entire range with predicted SOC concentration (Fig. 6f). For PET $/$ MAP, the predicted SOC content declined sharply as PET $/$ MAP increased from 1 to 2 (transition from wet to dry water regimes; Fig. 6g). The relationship between pH${}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ and predicted SOC content was not strong (Fig. 6h). For land cover, there was almost no difference between the classes within the same depth layer; however, topsoils had higher SOC content (2.2 wt %) compared with the subsoil samples across all land covers (1.5 wt %; Fig. 6i).

4 Discussion

Climate and geochemical variables are similarly important for explaining SOC variations across sub-Saharan Africa (Fig. 3), which is in line with findings from a global study (Luo et al., 2021). However, the explanatory power of climate and geochemical variables are not independent of each other, reflecting the overall strong interaction between climate and geochemistry (Doetterl et al., 2015). Since it is likely that, in the long term, climate variables have predominantly indirect effects on SOC dynamics through their influence on soil geochemistry, we focus our discussion on those geochemical variables (Ca_ex, Al_ox and Fe_ox) that showed the highest explanatory power with respect to SOC content across all models. In addition, we discuss the role of depth, clay + fine silt content and land cover in explaining SOC variations on a continental scale, since other studies have identified their important role in SOC dynamics.

4.1 Exchangeable calcium

Strong and positive relationships emerged between Ca_ex and SOC concentration across all models, even though Ca_ex concentration showed strong pH${}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ and precipitation dependence (Fig. 5). Typical Ca²⁺ sources in soils are from (a) weathering of bedrock or surface rock formations, (b) decomposition of Ca²⁺-rich organic materials, (c) lateral movement of Ca²⁺-rich water, (d) atmospheric dust and rain deposition or (e) anthropogenic inputs (Likens et al., 1998; Rowley et al., 2018). Characteristically, Ca²⁺ is weathered easily from both primary and secondary minerals (Likens et al., 1998). This usually leads to its accumulation in semi-arid to arid environments that are characterized by low rates of water flow through the soil profile that drives slow weathering rates and high pH${}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ values (Fig. 4b–d). In such environments, Ca²⁺ plays an important role as a cation bridge that facilitates aggregate formation (Rimmer and Greenland, 1976; Tisdall and Oades, 1982) and bonding of clay minerals to organic matter functional groups because of their divalent charge, relative abundance and modest hydration radius (Likens et al., 1998; Muneer and Oades, 1989). However, we found that Ca_ex was not only important in alkaline and less-weathered soils in dry regions but also in acidic and more-weathered soils under wetter conditions (Fig. 5). It is likely that the main Ca²⁺ source in those regions derives from atmospheric deposition (Albani et al., 2015; Goudie and Middleton, 2001) and/or biological cycling by plants (Likens et al., 1998). This is supported by the fact that Ca_ex showed a stronger relationship with SOC in topsoil than subsoil layers (Figs. 4a and 6b). Since land cover, which is a major driver of C inputs into the soil, did not show a strong relationship with SOC in the models, we speculate that biological cycling of Ca²⁺ does not play a major role in explaining the observed differences in SOC content. Yet, further analysis with better proxies for biological Ca²⁺ inputs is needed to test this hypothesis. High Ca²⁺ concentrations in acidic soils can also be derived from the development of those soils from Ca²⁺-rich parent material which are out of equilibrium with modern climate conditions (Slessarev et al., 2016).

In conclusion, the important role of Ca_ex in our data set was most pronounced in dry regions dominated by alkaline and less weathered soils. However, it also played a role in explaining the SOC variation in wetter regions and more acidic soils, which supports the overall importance of Ca_ex in stabilizing SOC.

4.2 Oxalate extractable Al and Fe

Similar to Ca_ex, short-range-order minerals (M_ox, Al_ox and Fe_ox) showed a positive and strong correlation with SOC content across all models. The relationship was strongest in wet regimes with acidic and highly weathered soils (Figs. 4b–d and 5b). Hydrous oxides of Al and Fe are usually highly reactive because of their large specific areas with a high proportion of reactive sites (Parfitt and Childs, 1988). This results in the adsorption of organic matter to Fe and Al oxides and the formation of stable soil aggregates (Tisdall and Oades, 1982). In humid regions, high rates of mineral weathering may release Fe, Al and Si faster than crystalline minerals can precipitate (Rasmussen et al., 2018). Therefore, Fe_ox and Al_ox are usually found to be important in SOC stabilization in humid and acidic soils (Eusterhues et al., 2003; Kramer and Chadwick, 2018).

In our study, short-range-order minerals were also identified to play an important role for SOC stabilization in soils of sub-Saharan Africa. However, even though Al_ox and Fe_ox showed similar trends in their concentrations (Fig. 5b), we observed diverging behavior in their predictive power of SOC in the regression trees (Fig. A6) and the random forests (Fig. 6a and e). For example, Fe_ox was one of the most important explanatory variables in the regression tree and partial dependence plots, although only within a very narrow range and at low Fe_ox concentrations (Fig. 6e), whereas Al_ox was important over the entire range (Fig. 6a). Inagaki et al. (2020) showed that higher amounts of soil organic matter were co-localized with Fe in drier regions compared to sites with higher rainfall, whereas the content of Al_ox co-localized with organic matter was not affected by precipitation changes. This may be linked to the different oxidation levels of Fe. At higher precipitation levels, Fe oxides can be reduced, resulting in a release of associated SOC to the aqueous phase (Berhe et al., 2012; Chen et al., 2020; Thompson et al., 2011). This mechanism is probably responsible for the low correlation between SOC and high Fe_ox concentrations in our data (Fig. 6e), pointing to the fact that Fe_ox can act as pedogenic threshold, depending on its oxidation level in the soil system.

In summary, short-range-order minerals also play an important role in SOC stabilization across sub-Saharan Africa, similar to other regions. However, Al_ox and Fe_ox do behave differently in explaining SOC content, even though they showed covariance in terms of their concentrations. Since we only have data for acid-oxalate extraction, we cannot speculate further about their diverging behavior in the models.

4.3 Depth

For the depth models, predictor differences were small between topsoil (0–20 cm) and subsoil (20–50 cm) samples (Figs. 4a and 6). This may reflect the large depth increments for each of the two sampling depths, which may also explain the overall small explanatory power of depth in the linear-mixed effects model (Fig. 3a). Since the identified SOC-controlling factors were similar for both depth layers (Fig. 4a), differences in SOC content were likely driven by the fact that subsoil samples usually contain less SOC due to lower C inputs at greater depth (Jobbágy and Jackson, 2000). Soil erosion at some sites (data not shown) might also dilute differences between the two depth layers, since water and wind can permanently remove surface soil.

4.4 Clay + fine silt content

Clay + fine silt content (<8 µm) did not emerge as an important predictor of SOC concentration within our different models (Figs. 3, 4 and 5e). This is in contrast to some earlier studies that indicated that total clay content explains a large proportion of SOC storage and stabilization due to the sorption of soil organic matter to surfaces of clay minerals and building of aggregates (Amelung et al., 1998; Kahle et al., 2002). The relationship between SOC and total clay content is used in various models to describe the turnover and storage of SOC. However, this simplified correlation may not account for the different stabilization mechanisms related to various clay minerals, e.g., 1:1 vs. 2:1 clay minerals (Oades, 1988). Past research has yielded contradictory results on whether clay content explains SOC variation in subtropical and tropical soils or not. For example, Bruun et al. (2010) showed, for various tropical soils, that clay mineralogy, Fe_ox and Al_ox are better explanatory variables for SOC content than clay content alone (<2 µm). In contrast, Quesada et al. (2020) found a strong relationship between clay and SOC content for highly weathered soils in the Amazon Basin that are dominated by 1:1 clay minerals, such as kaolinite, whereas soils in the same system, dominated by 2:1 clay minerals, showed stronger relationship between SOC and Al species. In a comparison between tropical and temperate soils, Six et al. (2002b) found that less C was associated with the clay and silt fraction (<20 µm) in tropical soils than in temperate soils. Even though these studies used various cut-offs to define the clay (<2 µm), clay + fine silt (<8 µm) and clay and silt fraction (<20 µm), they all illustrate that the relationship with SOC can be complex in subtropical and tropical soils.

Due to the broad spatial scale, soils in the AfSIS data set contain different clay minerals (Butler et al., 2020). No clear relationship between clay + fine silt content (<8 µm) and SOC concentration was observed in the models, although the raw data indicate an overall positive trend between clay + fine silt content (<8 µm) and SOC concentration (Fig. 2b). This positive relationship does not hold across all sites (Figs. 2c and A5). Variable relationships with SOC (Table B2) may explain the low predictive power of clay + fine silt content in this data set. Instead, variables that better capture the different behavior of clay-sized minerals, e.g., Ca_ex, Fe_ox and Al_ox, are likely more suitable soil parameters to explain the variation in SOC content – even in highly weathered soils across sub-Saharan Africa. This is supported by the fact that a clay + fine silt-only model resulted in a very small R² (0.01 – linear mixed-effects model; 0.12 – random forest; Table B3).

4.5 Land cover

The effect of land cover on SOC content was generally small in our models, even in topsoils (Fig. 6i). Similar findings were recently encountered in a global study (Luo et al., 2021). One possibility may be that the relatively large 0–20 cm depth interval might dilute differences that could be more marked in the top few centimeters. However, we did observe differences in SOC content across land cover classes, with forests containing the highest amount of SOC – especially in topsoils (Fig. 2a). Croplands had higher SOC content than grasslands, which is opposite of what is commonly observed in temperate regions (Prout et al., 2020).

Another possible explanation for the absence of land cover as an important predictor in our models, is that we lacked the detailed data necessary to disentangle the impacts of different practices and land use history. The land cover class cropland contained a wide variety of cultivated plots, while more detailed information about land management practices was missing. This is particularly important since prior research in other regions showed that SOC stock changes in tropical cropland soils may be driven by C inputs (Fujisaki et al., 2018b). Additionally, historical land use may even play a more important role in explaining current stocks compared to recent land use (Vågen et al., 2006).

Furthermore, land cover may covary with other parameters (temperature, precipitation and geochemistry) to such a degree that it is not an explanatory variable. This might be the reason why the submodels grouped by land cover did not show a clear pattern (Fig. 4e). However, the land-cover-only models resulted in small R² (0.01 – linear mixed-effects models; 0.10 to 0.16 – random forest), which suggests that land cover is a poor predictor for our SOC data at this large spatial scale (Table B3). This may be due to the high variation in SOC content within the different land cover classes (Fig. 2a). Land use changes and their impact on soil physico-chemical properties are scale dependent and likely to be more distinct at smaller scales (Holmes et al., 2004, 2005). For example, land management and land degradation (i.e., erosion) are known to impact SOC stocks at regional scales in sub-Saharan Africa (Winowiecki et al., 2016a).

Future studies are needed to better understand the impacts of land management and carbon storage potential in soils across sub-Saharan Africa at different scales (Fujisaki et al., 2018a; Vanlauwe et al., 2015). Overall, our data for sub-Saharan Africa suggests that SOC content on a continental scale is better explained by stabilization potential in soils (climate, geochemistry) than by different aboveground C inputs (vegetation).

5 Conclusions

We used a continental-scale data set from sub-Saharan Africa to test relationships between SOC content, various soil properties and climate variables in order to address our core research questions.

1. Which soil properties and climate parameters best explain SOC content variation across sub-Saharan Africa?

   Parameters similar to temperate regions best explain the variation in SOC content in tropical and subtropical soils under various climate conditions across sub-Saharan Africa, namely Ca_ex, M_ox (Al_ox and Fe_ox) and PET $/$ MAP. At this large spatial scale, climate and geochemical parameters are equally important and share some of the explained SOC variation. However, land cover and clay + fine silt content did not explain much of the variation in SOC content, in contrast to some findings from other regions and studies.

   The selected climatic and geochemical parameters, which can be seen as proxies for most of the soil-forming factors, explain about two-thirds of SOC variation across sub-Saharan Africa. The remaining third likely reflects those soil-forming factors that were not or only poorly represented within our selected variables, namely organisms, relief and time. However, given the large spatial scale of the study, even such additional information is unlikely to explain all of the SOC variation measured.

2. How do geochemical controls on SOC vary between environmentally distinct subregions?

   In dry regions with alkaline and less-weathered soils, Ca_ex explained most of the SOC concentration variation, whereas M_ox was more important in wetter regions with acidic and highly weathered soils. Still, Ca_ex remained important in acidic and more weathered soils and in wetter regions. Fe_ox, as a predictor of SOC content, was only important at low concentrations in moderately weathered and wet soils. This observed trend suggests that Fe_ox can play an important role in pedogenic thresholds in various soils across sub-Saharan Africa.

   Overall, a combination of PET $/$ MAP, Ca_ex and M_ox seems to be an appropriate set of variables to explain the SOC content variation on a continental scale across sub-Saharan Africa. This does not imply that other variables, such as clay + fine silt content and land cover are not good predictors on a regional scale, as shown by previous studies. However, the variables identified by this study showed a consistent predictive power of SOC content across various climate regions.

   Future studies on large-scale SOC stabilization should consider measuring these soil properties to include them in models. This would likely improve the predictive capacity of these models and contribute to closing the gap between our theoretical understanding of SOC concentration across large scales and our ability to improve terrestrial biogeochemical model projections.

Appendix A

The figures and tables on the next two pages all belong to the same topic. They show the results for the different cut-offs we used to identify the best cut-off to be used for soil texture. We looked at and tested for <2, <8 and <20 µm. In the end, we decided to use <8 µm because we wanted to stay as close as possible to <2 µm. However, we could not use <2 µm due to some reproducibility issues for duplicates. The differences between <8 and <20 µm are negligible.

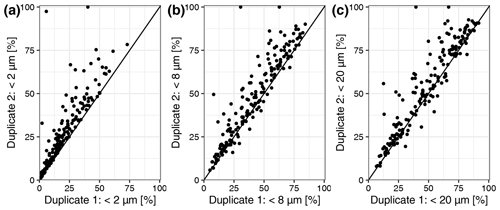
Figure A1 Scatterplot of duplicate measurements for the particle size distribution data. (a) Duplicate 1 and 2 <2 µm. (b) Duplicate 1 and 2 <8 µm. (c) Duplicate 1 and 2 <20 µm.

Table A1 Correlation coefficient between SOC and particle size data <8 and <20 µm for all samples (n=1601), topsoil (0–20 cm; n=791) and subsoil (20–50 cm; n=810).

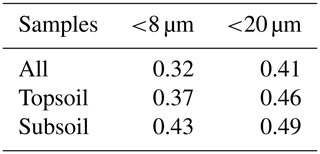
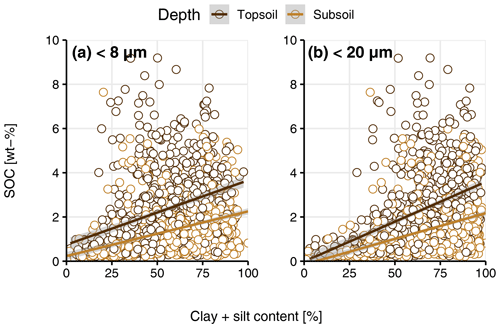
Figure A2 (a) Soil organic carbon (SOC) content (wt %) and clay + fine silt content <8 µm (percent) by depth. (b) SOC content (wt %) clay + fine silt content <20 µm (percent) by depth.

Table A2 Summary table of R² for the different models (linear mixed-effects model and random forest) for the two different explanatory variables (<8 and <20 µm) for all samples (n=1601), topsoil (0–20 cm; n=791) and subsoil (20–50 cm; n=810).

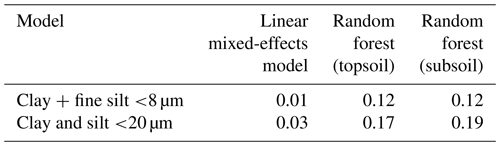
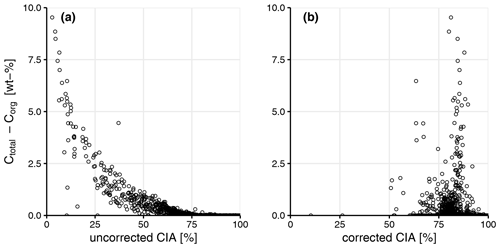
Figure A3 Scatterplot of inorganic carbon (C_total–C_org; wt %), the uncorrected chemical index of alteration (CIA; percent) a) and the CIA (percent) correct for carbonates and apatite after Nesbit and Young (1982) (b). See Sect. 2 for more details.

Figure A4 Spatial visualization of selected training (blue) and test (orange) observations for spatial cross-validation of two repetitions from the topsoil samples. Note: each dot may represent multiple samples.

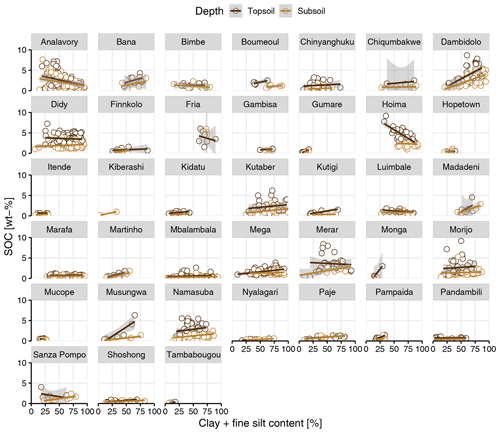
Figure A5 Soil organic carbon (SOC; wt %) and clay + fine silt content (percent) by depth for each sampling site that contained more than one sample per depth layer (0–20 cm – topsoil; 20–50 cm – subsoil). The gray area around fitted linear regressions represents the 95 % confidence interval.

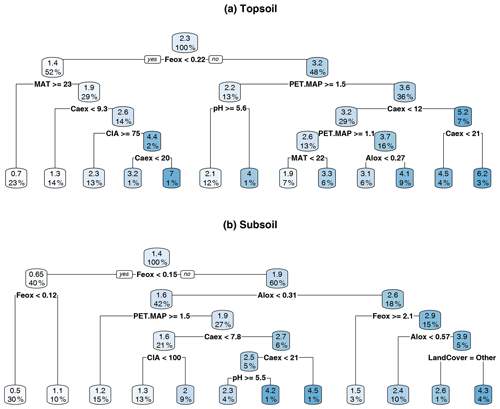
Figure A6 Regression tree for (a) topsoil (0–20 cm) and (b) subsoil (20–50 cm). Splitting values are always in the units of the parameter used for the split (for units, see Table 1). Absolute values in the boxes indicate the predicted soil organic carbon (SOC) content (wt %). The percentage corresponds to the relative number of samples.

Appendix B

Table B1 Overview of sample distribution used in this study across geographical regions, countries, sites, depths and land cover.

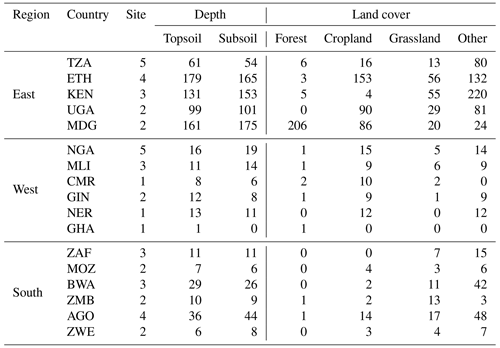
TZA – Tanzania; ETH – Ethiopia; KEN – Kenya; UGA – Uganda; MDG – Madagascar; NGA – Nigeria; MLI – Mali; CMR – Cameroon; GIN – Guinea; NER – Niger; GHA – Ghana; ZAF – South Africa; MOZ – Mozambique; BWA – Botswana; ZMB – Zambia; AGO – Angola; ZWE – Zimbabwe.

Table B2 Marginal R² for each fixed effect based on sequential fitting of the linear mixed-effects models for the different submodels (depth, pH classes, number of wet months, weathering and land cover). The sign in parentheses refers to the correlation between the fixed effect and soil organic carbon, respectively. Bold values have a p value < 0.0001 based on likelihood ratio test.

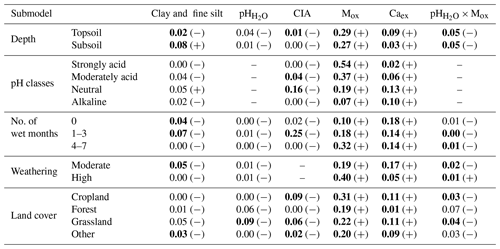
CIA – chemical index of alteration; M_ox – oxalate-extractable metals (Al_ox+ $\mathrm{1}/\mathrm{2}$ Fe_ox).

Table B3 Summary table of R² for the different models (linear mixed-effects model and random forest) with different explanatory variables (clay + fine silt, land cover, clay + fine silt and land cover and full) included for the entire data set. The R² in parentheses for the linear mixed-effects models refer to the conditional R², which include the variation explained by the random effects (siteID/clusterID/plotID).

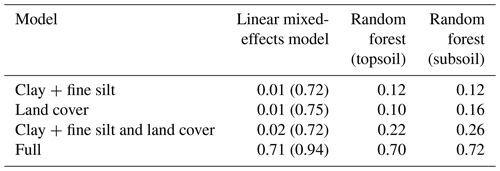
Table B4 Analysis of variance (ANOVA) summary for linear mixed-effects analyses with the entire data set (n=1601), including all predictors and geochemistry-only and climate-only predictors. Fixed effects were added using a step-wise method. The first entry (∼ 1) refers to the constant null model, respectively.

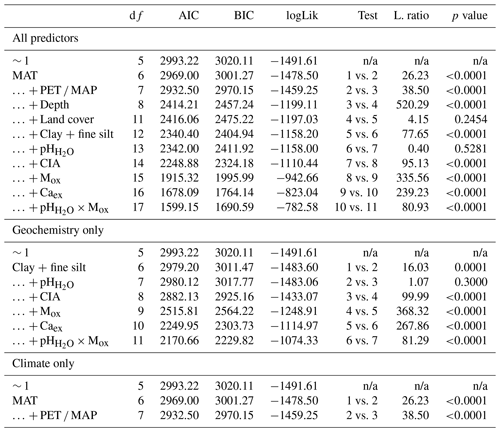
MAT – mean annual temperature; PET – potential evapotranspiration; MAP – mean annual precipitation; CIA – chemical index of alteration; M_ox – oxalate-extractable metals (Al_ox+ $\mathrm{1}/\mathrm{2}$ Fe_ox); Ca_ex – exchangeable calcium; n/a – not applicable; df:– degree of freedom; AIC – Akaike information criterion; BIC – Bayesian information criterion; logLik – log likelihood; L.ratio – likelihood ratio.

Table B5 ANOVA summary for linear mixed-effects grouped by depth (n_Topsoil=791; n_Subsoil=810). Fixed effects were added using a step-wise method. The first entry (∼ 1) refers to the constant null model, respectively.

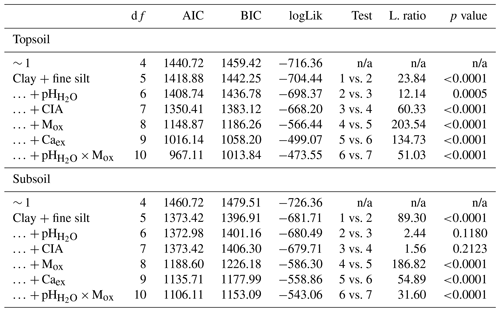
MAT – mean annual temperature; PET – potential evapotranspiration; MAP – mean annual precipitation; CIA – chemical index of alteration; M_ox – oxalate-extractable metals (Al_ox+ $\mathrm{1}/\mathrm{2}$ Fe_ox); Ca_ex – exchangeable calcium; n/a – not applicable; df:– degree of freedom; AIC – Akaike information criterion; BIC – Bayesian information criterion; logLik – log likelihood; L.ratio – likelihood ratio.

Table B6 ANOVA summary for linear mixed-effects grouped by pH${}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ (n_{strongly acidic}=404; n_{moderately acidic}=399; n_neutral=398; n_alkaline=400). Fixed effects were added using a step-wise method. The first entry (∼ 1) refers to the constant null model, respectively.

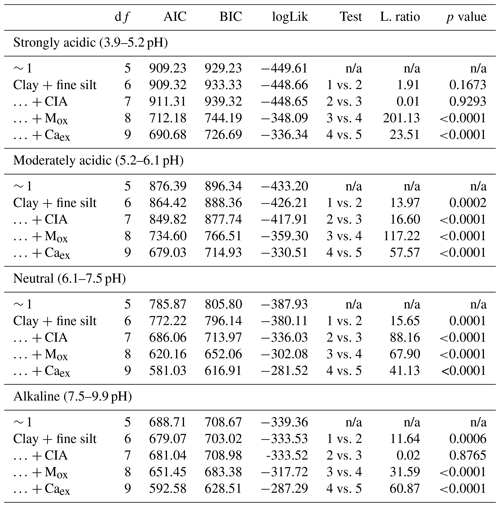
MAT – mean annual temperature; PET – potential evapotranspiration; MAP – mean annual precipitation; CIA – chemical index of alteration; M_ox – oxalate-extractable metals (Al_ox+ $\mathrm{1}/\mathrm{2}$ Fe_ox); Ca_ex – exchangeable calcium; n/a – not applicable; df:– degree of freedom; AIC – Akaike information criterion; BIC – Bayesian information criterion; logLik – log likelihood; L.ratio – likelihood ratio.

Table B7 ANOVA summary for linear mixed-effects grouped by the number of wet months (P $/$ PET >1; n₀=572, $n_{\mathrm{1}-\mathrm{3}}=\mathrm{367}$, $n_{\mathrm{4}-\mathrm{7}}=\mathrm{662}$). Fixed effects were added using a step-wise method. The first entry (∼ 1) refers to the constant null model, respectively.

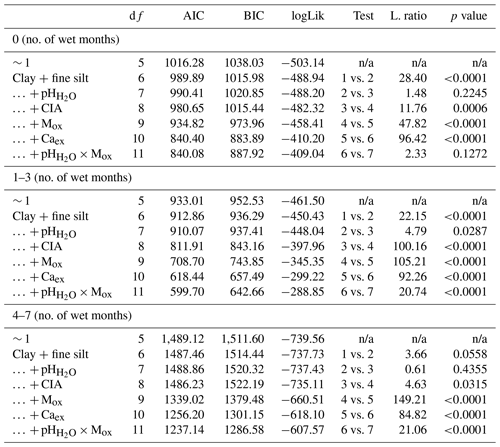
MAT – mean annual temperature; PET – potential evapotranspiration; MAP – mean annual precipitation; CIA – chemical index of alteration; M_ox – oxalate-extractable metals (Al_ox+ $\mathrm{1}/\mathrm{2}$ Fe_ox); Ca_ex – exchangeable calcium; n/a – not applicable; df:– degree of freedom; AIC – Akaike information criterion; BIC – Bayesian information criterion; logLik – log likelihood; L.ratio – likelihood ratio.

Table B8 ANOVA summary for linear mixed-effects grouped by weathering (n_moderate=801; n_high=800). Fixed effects were added using a step-wise method. The first entry (∼ 1) refers to the constant null model, respectively.

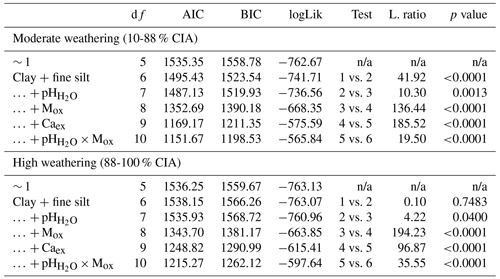
MAT – mean annual temperature; PET – potential evapotranspiration; MAP – mean annual precipitation; CIA – chemical index of alteration; M_ox – oxalate-extractable metals (Al_ox+ $\mathrm{1}/\mathrm{2}$ Fe_ox); Ca_ex – exchangeable calcium; n/a – not applicable; df:– degree of freedom; AIC – Akaike information criterion; BIC – Bayesian information criterion; logLik – log likelihood; L.ratio – likelihood ratio.

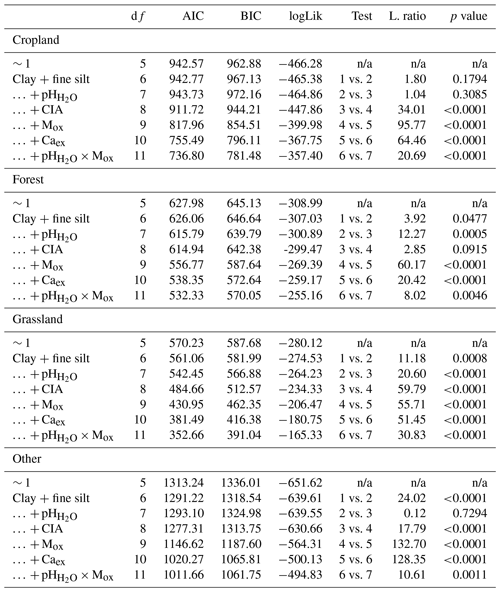
Table B9 ANOVA summary for linear mixed-effects grouped by land cover (n_Cropland=429; n_Forest=228; n_Grassland=242; n_Other=702). Fixed effects were added using a step-wise method. The first entry (∼ 1) refers to the constant null model, respectively.

MAT – mean annual temperature; PET – potential evapotranspiration; MAP – mean annual precipitation; CIA – chemical index of alteration; M_ox – oxalate-extractable metals (Al_ox+ $\mathrm{1}/\mathrm{2}$ Fe_ox); Ca_ex – exchangeable calcium; n/a – not applicable; df:– degree of freedom; AIC – Akaike information criterion; BIC – Bayesian information criterion; logLik – log likelihood; L.ratio – likelihood ratio.