Comparing three approaches of spatial disaggregation of legacy soil maps based on the Disaggregation and Harmonisation of Soil Map Units Through Resampled Classification Trees (DSMART) algorithm

Enhancing the spatial resolution of pedological information is a great challenge in the field of digital soil mapping (DSM). Several techniques have emerged to disaggregate conventional soil maps initially and are available at a coarser spatial resolution than required for solving environmental and agricultural issues. At the regional level, polygon maps represent soil cover as a tessellation of polygons defining soil map units (SMUs), where each SMU can include one or several soil type units (STUs) with given proportions derived from expert knowledge. Such polygon maps can be disaggregated at a finer spatial resolution by machine-learning algorithms, using the Disaggregation and Harmonisation of Soil Map Units Through Resampled Classification Trees (DSMART) algorithm. This study aimed to compare three approaches of the spatial disaggregation of legacy soil maps based on DSMART decision trees to test the hypothesis that the disaggregation of soil landscape distribution rules may improve the accuracy of the resulting soil maps. Overall, two modified DSMART algorithms (DSMART with extra soil profiles; DSMART with soil landscape relationships) and the original DSMART algorithm were tested. The quality of disaggregated soil maps at a 50 m resolution was assessed over a large study area (6775 km²) using an external validation based on 135 independent soil profiles selected by probability sampling, 755 legacy soil profiles and existing detailed 1:25 000 soil maps. Pairwise comparisons were also performed, using the Shannon entropy measure, to spatially locate the differences between disaggregated maps. The main results show that adding soil landscape relationships to the disaggregation process enhances the performance of the prediction of soil type distribution. Considering the three most probable STUs and using 135 independent soil profiles, the overall accuracy measures (the percentage of soil profiles where predictions meet observations) are 19.8 % for DSMART with expert rules against 18.1 % for the original DSMART and 16.9 % for DSMART with extra soil profiles. These measures were almost 2 times higher when validated using 3×3 windows. They achieved 28.5 % for DSMART with soil landscape relationships and 25.3 % and 21 % for original DSMART and DSMART with extra soil observations, respectively. In general, adding soil landscape relationships and extra soil observations constraints allow the model to predict a specific STU that can occur in specific environmental conditions. Thus, including global soil landscape expert rules in the DSMART algorithm is crucial for obtaining consistent soil maps with a clear internal disaggregation of SMUs across the landscape.

1 Introduction

Characterising soil variability, especially over large areas, remains a crucial challenge for fostering the sustainable management of agronomic and environmental issues and helping stakeholders to design regional projects (Chaney et al., 2016). At the regional and country level, soil maps are often available at a coarse spatial resolution (Bui and Moran, 2001) which limits their ability to depict accurate soil information. For instance, the finest soil maps covering France were extended to include administrative regions at a 1:250 000 scale, via a set of polygons, called soil map units (SMUs) with crisp boundaries. The delineation of SMUs is based on soil survey programmes involving pedologists' expertise. In a coarse-scale map, each polygon includes one or several soil type units (STUs), which are not explicitly mapped, but their proportions, environmental conditions and soil characteristics are provided in a detailed database (Le Bris et al., 2013).

To improve soil variability knowledge and to overcome the limitations of a coarse mapping scale, several methods have emerged in the field of digital soil mapping (DSM). These methods offer useful tools for predicting soil spatial patterns from scarce or limited soil data sets by exploiting the availability of model-based methods and an extensive array of spatialised (and, more often than not, gridded) environmental variables. In recent decades, DSM techniques have been increasingly used to downscale soil information and improve their spatial resolution. Depending on the quality of the data and the complexity of soil cover, Minasny and McBratney (2010) have supplied a workflow that outlines the different models that can be explored. In general, two main pathways can be distinguished, namely point-based DSM approaches and map-disaggregation approaches (Odgers et al., 2014; Holmes et al., 2015). Point-based DSM approaches use legacy soil profiles, which are irregularly distributed and collected according to specific objectives rather than optimising a statistical criterion (Holmes et al., 2015). The spatial distribution of soil properties can be estimated by fitting geostatistical models such as ordinary kriging (Odgers et al., 2014; Holmes et al., 2015; Chaney et al., 2016; Santra et al., 2017; Vincent et al., 2018; Chen et al., 2018) or co-kriging, which takes into account the spatial interrelations among several soil properties (Webster and Oliver, 2007). Additionally, McBratney et al. (2003) formalised the Soils, Climate, Organisms, Parent material, Age and (N) space or spatial position (SCORPAN) soil landscape model. It is an empirical quantitative function of environmental covariates allowing the prediction of soil attributes (soil type or soil property) based on correlative and statistical relationships with predictor variables.

The second approach, known as spatial disaggregation, attempts to downscale the soil map unit information in order to delineate unmapped STUs (Bui and Moran, 2001; Odgers et al., 2014; Holmes et al., 2015). Alternatively, it can be defined as the process that allows the estimation of soil properties at a finer scale than that of the initial soil map. Several techniques have been demonstrated in soil science literature and tested in different case studies around the world. For instance, Kempen et al. (2009) have explored the use of multinomial logistic regression (MLR) for digital soil mapping. Other techniques have also been applied as decision trees using rule-based induction (Bui and Moran, 2001), Bayesian techniques (Bui et al., 1999) and an area-to-point kriging method (Kerry et al., 2012).

In the DSM field, machine-learning techniques are increasingly used to elucidate the spatial distribution of both soil type and soil properties across a large range of scales (Bui and Moran., 2001; Scull et al., 2005; Malone et al., 2009; Nelson and Odeh, 2009; Abdel-Kader, 2011; Lacoste et al., 2011; Lemercier et al., 2012; Kempen et al., 2012; Jafari et al., 2013; Nauman and Thompson, 2014; Brungard et al., 2015; Mosleh et al., 2016; Viloria et al., 2016; Nussbaum et al., 2018; Vaysse and Lagacherie, 2015; Ellili et al., 2019; Padarian et al., 2019; Arrouays et al., 2020).They were also applied to disaggregate superficial geology maps available at a 1:250 000 scale in Australia (Bui and Moran, 2001). The main advantage of these approaches is they allow the handling of both quantitative and categorical (ordinal or nominal) soil and environmental variables as explanatory covariates (Bui and Moran, 2001).

Odgers et al. (2014) have developed a machine-learning algorithm entitled the Disaggregation and Harmonisation of Soil Map Units Through Resampled Classification Trees (DSMART) to predict STUs as a function of the high-resolution environmental data supplied over different study areas in Australia. The DSMART algorithm is based on a calibration data set derived from a random selection of a fixed number of sampling points within each soil polygon. Each sampling point is then assigned to one soil type following a weighted random allocation procedure based on the proportions informed by the soil map database. The same procedure was applied by Chaney et al. (2016) to spatially disaggregate the soil map of the contiguous United States of America at a 30 m spatial resolution. Because the integration of pedological knowledge has been recognised as an effective way to improve digital soil mapping approaches (Cook et al., 1996; Walter et al., 2006; Stoorvogel et al., 2017; Machado et al., 2018; Møller et al., 2019; Arrouays et al., 2020), Vincent et al. (2018) have applied the DSMART algorithm with additional expert soil landscape rules describing the soil distribution in the local context of the Brittany region (France). By adding supplementary sampling points to the calibration data set selected according to the soil parent material, soil redoximorphic conditions and topographic features, and by integrating soil landscape relationships in the DSMART sample allocation scheme, the authors obtained a coherent soil spatial distribution that observed the soil organisation along hill slopes and the occurrence of intensely waterlogged soils in the stream neighbourhood, as seen in Brittany.

This study aimed to test the hypothesis that adding soil landscape relationships to the disaggregation procedure improved the accuracy of the disaggregated soil maps produced. This involved assessing the contribution of soil landscape relationships implemented in the DSMART algorithm by Vincent et al. (2018). To achieve this objective, we compared disaggregated soil maps either derived from the original DSMART algorithm, the DSMART algorithm with extra soil observations or the DSMART algorithm fed by soil landscape relationships over an area of 6775 km² in the eastern part of Brittany, France.

2 Materials and methods

2.1 Study area

The Ille-et-Vilaine region covers an area of 6775 km² and is located in the eastern part of Brittany, France (48^∘ N, 2^∘ W; Fig. 1). It is drained by the rivers Ille and Vilaine and their tributaries. Its climate is oceanic, with a mean annual rainfall of 669 mm and mean annual temperature of 11.3^∘ (Source: Climate Data EU). Main land uses include arable land, temporary and permanent grasslands, woodlands and urban areas. In the present study, anthropogenic areas were not considered. Elevation ranges between 0 and 20 m in the coastal zone and 20–150 m almost everywhere else, except in the western part of the region where it tills at 256 m. The topography is generally gentle, with maximum slopes not exceeding 16 %. The Ille-et-Vilaine region is part of the Armorican Massif, with complex geology (BRGM, 2009) including intrusive rocks (granite, gneiss and mica schist) in the northern and northwestern zones, sedimentary rocks (sandstone) and metamorphic rocks (Brioverian schist) in the central and southern zones, and superficial deposits (aeolian loam with decreasing thickness from north to south overlaying the bedrock, alluvial and colluvium deposits). According to the World Reference Base for Soil Resources, soils occurring in Ille-et-Vilaine include Cambisols, Luvisols Stagnic Fluvisols, Histosols, Podzols and Leptosols (IUSS Working Group WRB, 2014).

Figure 1 Location of the study area and the validation data sets.

2.2 Soil data

2.2.1 Regional soil database at 1:250 000 scale

In Brittany, soils are represented through a regional geographic database called the Référentiel Régional Pédologique (RRP) and available at a 1:250 000 scale (INRA Infosol, 2014). This regional database identifies soils within soil map units (SMUs), each containing one to several soil types called soil type units (STUs). STUs are defined as areas with homogeneous soil-forming factors such as morphology, geology and climate. In the study area, 96 SMUs and 171 STUs have been distinguished and represented by a spatial coverage of 479 polygons. The STU nomenclature respects the French soil classification system (Baize and Girard, 2008). It reflects different information simultaneously like the weathering degree of the soil parent material, the redoximorphic conditions and the soil type, which refers to the identification of diagnostic horizons depicting pedogenetic processes and the soil depth.

In the regional database SMUs were spatially delimited with crisp boundaries while STUs were not explicitly mapped, but their proportion in each SMU and the associated environmental and soil characteristics were accurately described in a semantic database (Le Bris et al., 2013; INRA Infosol, 2014).

2.2.2 Soil validation data

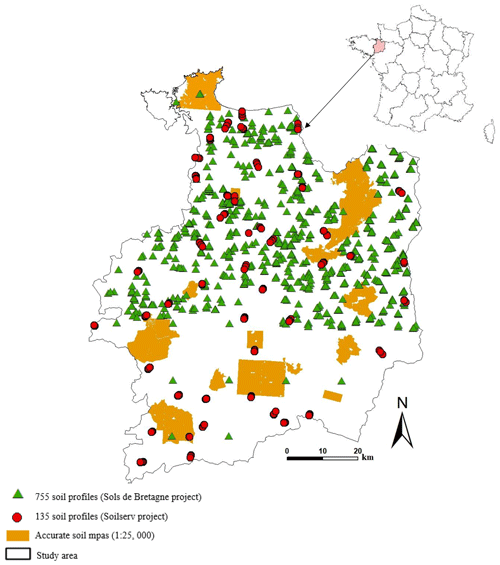
To assess the quality of disaggregated soil maps, three validation data sets were used (Fig. 1) as follows:

• A total of 135 soil profiles were chosen following a stratified random sampling design and specifically described and sampled from March to May 2017 for independent validation purposes in the framework of the Soilserv research project (Ellili-Bargaoui et al., 2019).

• A total of 755 legacy soil profiles were collected between 2005 and 2008 during the Sols de Bretagne programme (INRA Infosol, 2014). These profiles were sampled following a purposive sampling design, created by expert soil surveyors, to characterise the hydromorphic soil conditions and soil landscape heterogeneity.

• Existing detailed soil maps (1:25 000) covering 87 150 ha were surveyed according to Rivière et al. (1992) and revised later to adapt to the STU typologies developed in the RRP (Le Bris et al., 2013).

All soil profiles were allocated, after description and analysis by an expert, to a suitable STU. Both legacy soil profiles and detailed maps were converted to a raster format to perfectly meet the prediction raster at a 50 m spatial resolution.

2.3 Environmental covariates

The SCORPAN concept (McBratney et al., 2003) allows one to predict STUs as a function of a set of covariates describing seven soil-forming factors, namely soil properties (s), climate (c), organisms (o), relief (r), parent material (p), age (a) and geographic position (n). In this study, 10 environmental variables (Table 1) were considered as covariates in the disaggregation process at a 50 m spatial resolution, and they were chosen based on prior expert knowledge of the study area. Terrain attributes included elevation, slope, compound topographic index (CTI; Beven and Kirkby, 1979; Merot et al., 1995) and the topographic position index (TPI; Jenness, 2006; Vincent et al., 2018) that, together, were derived from a 50 m resolution digital elevation model (IGN, 2008). These attributes were computed using ArcGIS 10.1 (ESRI, 2012) and MNT surf software (Squividant, 1994).

Table 1 Description of the environmental covariates selected.

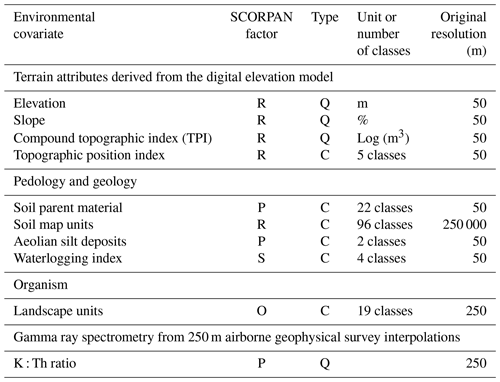
Summary of environmental covariates: P – parent material; S – soil properties; R – relief; O – organisms; C – categorical; and Q – quantitative.

Environmental attributes describing soil parent material (Lacoste et al., 2011) and hydromorphic soil conditions via the waterlogging index (Lemercier et al., 2012) were obtained using decision tree methods. The waterlogging index derives from a natural soil drainage prediction. Four classes were distinguished, namely well drained, moderately drained, poorly drained and very poorly drained. Aeolian silt deposits and soil map unit boundaries are environmental covariates also obtained via expert knowledge from soil scientists.

Landscape units reflecting vegetation, land use and relief attributes were derived from the Moderate Resolution Imaging Spectroradiometer (MODIS) imagery by supervised classification (Le Du Blayo et al., 2008). The airborne gamma ray spectrometry variable (K : Th ratio; Messner, 2008), characterising the degree of weathering of the geological material, was also considered.

All soil environmental covariates were converted to a raster format at a 50 m spatial resolution.

2.4 Disaggregation procedure: DSMART algorithm

2.4.1 Original DSMART algorithm (method 1)

The open source DSMART algorithm (Odgers et al., 2014) was applied to spatially disaggregate the existing legacy soil map at a 1:250 000 scale. The DSMART algorithm uses machine-learning classification trees implemented in C5.0 (Quinlan, 1993) to build a decision tree from a target variable (STUs) and the environmental covariates supplied. The DSMART algorithm was written in the Python programming language by Odgers et al. (2014) and was recently translated to the R programming language.

Running the DSMART algorithm requires the following three main steps (Fig. 2):

1. Polygon sampling by a random selection of a fixed number of sampling points (n=30) within each polygon. This procedure allowed for the selection of a total of 14 370 sampling points per iteration which covered the study area and ensured that all polygons were sampled.

2. Soil type unit (STU) assignment to each sampling point following a weighted random allocation method. This step was based on the proportion of each STU informed by the RRP database.

3. Decision tree generation once the full set of sampling points had been spatially intersected with the selected environmental covariates. This geo-referenced data set was then used as a calibration data set to build the decision tree, which allowed the prediction of an STU as a function of environmental covariates. C5.0 created explicit models which were applied to the covariates rasters to generate a realisation of the STU distribution over the study area at a 50 m resolution.

These three steps were repeated 100 times to generate 100 realisations of the potential soil type distribution over the study area at a 50 m resolution.

To compute the probabilities of occurrence, the 100 realisations were stacked to calculate the probability of occurrence of each predicted STU by counting the frequency of each STU at each pixel. This procedure led to a set of 171 rasters depicting the probability of occurrence for 171 STUs.

2.4.2 Original DSMART algorithm and soil observations (method 2)

This disaggregation approach is similar to the original DSMART algorithm. However, the main difference is that 755 additional soil profiles, spatially co-located, were added to the calibration data set to build decision trees. These soil profiles make it possible to incorporate real field observations into established soil landscape relationships. For each realisation, a calibration data set (15 125 samples), including virtual samples randomly selected from polygon units, and soil observations were used to model soil types with environmental covariates. From this fitted model we computed predictions for each node of the 50 m grid throughout the study area.

2.4.3 Original DSMART algorithm and expert rules (method 3)

Including soil landscape relationships in the disaggregation process was explored by Vincent et al. (2018) in a specific regional pedoclimatic context in Brittany (France). Expert soil landscape relationships were used to assign STUs to sampling points. These relationships were based on expert pedological knowledge, which considers the soil parental material and topography and waterlogging in the STU-allocation procedure. This approach combines two sources of the data set to calibrate the model. The first one was derived from semantic information for each SMU–STU combination. It consists of attributing a barcode to each SMU–STU combination, derived from a concatenation of four features contained in the RRP database (namely soil parent material, SMU identifier, TPI and waterlogging index), and comparing these barcodes to a stack of regional covariates representing the same four features and then assigning each pixel of the study area to a suitable STU. This procedure allowed the matching of soils exhibiting specific features with their potential spatial distribution. For instance, hydromophic soils occur with slope sequences and valley positions, while well-drained soils occur in upslope or mid-slope positions. Using a random sampling stratified by the SMU area, a set of sampling points was selected with a proportion of one sample for every 5 h and a minimum of five samples per polygon unit (3950 virtual samples).

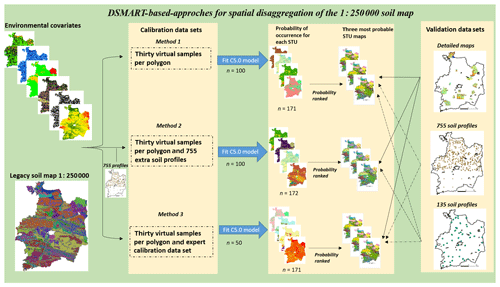
Figure 2 Schematic of the DSMART-based approaches algorithm. The steps in DSMART are as follows: method 1 – construct the calibration data set; method 2 – train the C5.0 model; and method 3 – estimate the STU maps and their associated probabilities of occurrence.

The second data set was derived from a random sampling of a fixed number of sampling points in each polygon unit. This procedure ensured that all polygons had been sampled. The STU allocation was based on the SMU area proportions. The full set of each realisation (18 320 samples), combining the expert calibration data set (3950 samples) and the data set derived from the random sampling procedure (14 370 virtual samples), was spatially intersected with existing environmental covariates and used as a calibration data set to build decision trees.

2.4.4 Prediction of the most probable STUs

From all the soil type probability rasters obtained, only the three most probable STUs (with the highest probability of occurrence) were considered; for each pixel, the final prediction was the combination of the three most probable predicted STUs (first, second and third STUs) and their associated probability of occurrence.

The classification confusion index (CI) between the first most probable STU and the second most probable STU was calculated in the following Eq. (1):

$$\begin{array}{}\text{(1)}& \mathrm{CI}=\mathrm{1}-\left(P_{\mathrm{st}\mathrm{STU}}-P_{\mathrm{2}\mathrm{nd}\mathrm{STU}}\right),\end{array}$$

where P_1st STU and P_2nd STU denote, respectively, the highest probability of occurrence for the first STU and the second-highest probability of occurrence for second STU calculated at each pixel (Burrough et al., 1997; Odgers et al., 2014).

This index was considered to be an indicator of the certainty assessment of the most probable predicted soil class and ranges between 0 and 1. It tends to 1, when the first and second STUs are predicted with a similar probability of occurrence, and 0, when the probability of occurrence of the second STU is close to 0.

2.5 Validation of disaggregated soil maps

The quality of soil maps resulting from the three DSMART algorithm-based approaches was assessed by combining both spatial- and semantical-validation methods. Spatial validation is divided into two sub-approaches, namely pixel to pixel and window of 3×3 pixels. For detailed soil maps and accurate soil profiles, the pixel-to-pixel validation consists of checking, at each pixel, if the predicted STU respects the observed STU value (Heung et al., 2014; Nauman et al., 2014; Chaney et al., 2016; Møller et al., 2019). The window-of-3×3-pixels validation assumes that, for each pixel, the predicted STU respects the observed STU value if it matches at least one of its nine surrounding neighbours (Heung et al., 2014; Chaney et al., 2016). This method provides some flexibility by compensating for the spatial referencing error of soil maps and avoiding the impact of fine-scale spatial noise.

The semantical validation was also performed by considering either each STU or a group of STUs sorted by experts on the basis of similar pedogenesis factors and similar diagnostic horizons (Vincent et al., 2018; Møller et al., 2019). From the initial 171 STUs described in the soil database, the sorting procedure led to 78 groups and 11 STUs remained single.

In this study, the validation data set with 755 observations was used to assess the accuracy of the digital maps derived from method 1 and method 3, but it was used as an additional calibration data set for method 2.

Moreover, to assess the performance of the three DSMART-based approaches, the confusion matrix was used to derive the Kappa index. This Kappa index corresponds to a chance-corrected index of the agreement between observed and predicted soil types (Cohen, 1960; Elith et al., 2008). It assumes values between −1 and 1; the higher the value, the better the prediction (Bergeri et al., 2002).

2.6 Pairwise comparisons of disaggregated soil maps

To compare the soil type rasters derived from the three DSMART-based approaches, pairwise comparisons were performed using the V_measure method implemented as open source software in an R package called the Spatial Association Between REgionalizations (SABRE; Rosenberg and Hirschberg, 2007). This is a spatial method developed to compare maps in the form of vector objects, and it was commonly used in computer science to compare (nonspatial) clustering.

We divided the entire study area into two different sets of regions referred to as regionalisation R and Z. The first regionalisation, R, divides the domain into n regions r_i (i=1 to n), and the second regionalisation, Z, divides the domain into m zones z_j (j=1 to m). The superposition of the two regionalisations, R and Z, divides the domain into n×m segments with a_ij area. The total area of a region r_i is $A_i={\sum }_{j,\mathrm{1}}^m{a}_{ij}$, the total area of a zone z_j is $Aj={\sum }_{i,\mathrm{1}}^n{a}_{ij}$ and the total of the domain is $A={\sum }_{j=\mathrm{1}}^m{\sum }_{i=\mathrm{1}}^n{a}_{ij}$.

The SABRE package calculates the degree of the spatial agreement between two regionalisations using an information theoretical measure called the V_measure. V_measure provides two intermediate metrics, namely homogeneity and completeness. Homogeneity is a measure of how well the regions from the first map fit inside the zones from the second map Eq. (2). Completeness measures how well the zones from the second map fit inside the regions from the first map Eq. (5). The final value of V_measure is calculated as the weighted harmonic mean of the homogeneity and completeness Eq. (8). All metrics range between 0 and 1, where larger values indicate a better spatial agreement. V_measure, homogeneity and completeness are global measures of association between the two regionalisations.

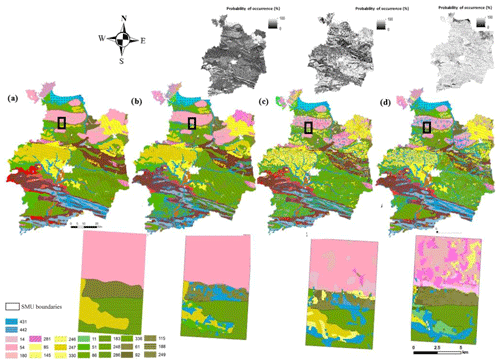
Figure 3 Digital soil map of the most probable STUs and their associated probability of occurrence for the whole study area and for a focus zone. The legacy soil map shows the (a) most probable STUs for each SMU, (b) original DSMART approach, (c) DSMART with expert rules and (d) DSMART with extra soil observations.

Additional indicators of the disaggregation quality were calculated using the Shannon entropy index of regions and zones (Shannon, 1948; Nowosad and Stepinski, 2018). These indicators qualify local associations by highlighting the region's inhomogeneities (Eqs. 3–4) or the zone's inhomogeneities (Eqs. 6–7). Two normalised Shannon entropies were also computed using the ratios ($S_j^R/S^R$) and ($S_i^Z/S^Z$) to derive maps of local spatial agreement between the two regionalisations of R and Z. These measures have a range between 0 and 1.

When $S_j^R$ in Eq. (3) is close to zero, this denotes that the zone j is homogenous in terms of the regions (each zone is within a single region). However, when the $S_j^R$ value increases, the zone is increasingly inhomogeneous in terms of the regions (it overlays an increasing number of regions). Therefore, $S_j^R$ Eq. (3) assesses the degree of this inhomogeneity or a variance of the region in zone j. A global indicator that measures the homogeneity of a given zone in terms of regions is given via Eq. (2).

Analogous to homogeneity, but with the roles of regions and zones reversed, the dispersion of zones over the entire area is also computed using a Shannon entropy (Eqs. 4 and 7), and a global indicator of C Eq. (5) measures the homogeneity of a given region in terms of zones as follows:

$$\begin{array}{}\text{(2)}& {\displaystyle }\begin{array}{rl}h=& \mathrm{1}-{\sum }_{j=\mathrm{1}}^m\left({\displaystyle \frac{A_j}{A}}\right)\\ & \left({\displaystyle \frac{\mathrm{Variance}\mathrm{of}\mathrm{regions}\mathrm{in}{\mathrm{zone}}_j=S_j^R}{\mathrm{Variance}\mathrm{of}\mathrm{regions}\mathrm{in}\mathrm{the}\mathrm{domain}=S^R}}\right)\end{array}\text{(3)}& {\displaystyle }{S}_j^R=-{\sum }_{i=\mathrm{1}}^n\left({\displaystyle \frac{a_{i,j}}{A_j}}\right)\log \left({\displaystyle \frac{a_i{,}_j}{A_j}}\right)\text{(4)}& {\displaystyle }{S}^R=-{\sum }_{i=\mathrm{1}}^n\left({\displaystyle \frac{A_i}{A}}\right)\log \left({\displaystyle \frac{A_i}{A}}\right)\text{(5)}& {\displaystyle }\begin{array}{rl}c=& \mathrm{1}-{\sum }_{i=\mathrm{1}}^n\left({\displaystyle \frac{A_i}{A}}\right)\\ & \left({\displaystyle \frac{\mathrm{Variance}\mathrm{of}\mathrm{zones}\mathrm{in}{\mathrm{region}}_i=S_i^Z}{\mathrm{Variance}\mathrm{of}\mathrm{zones}\mathrm{in}\mathrm{the}\mathrm{domain}=S^Z}}\right)\end{array}\text{(6)}& {\displaystyle }{S}_i^Z=-{\sum }_{j=\mathrm{1}}^m\left({\displaystyle \frac{a_{i,j}}{A_i}}\right)\log \left({\displaystyle \frac{a_i{,}_j}{A_i}}\right)\text{(7)}& {\displaystyle }{S}^Z=-{\sum }_{j=\mathrm{1}}^m\left({\displaystyle \frac{A_j}{A}}\right)\log \left({\displaystyle \frac{A_j}{A}}\right)\text{(8)}& {\displaystyle }{V}_{\mathit{\beta }}={\displaystyle \frac{\left(\mathrm{1}+\mathit{\beta }\right)hc}{\left(\mathit{\beta }h\right)+c}}.\end{array}$$

β is a coefficient that allows the promotion of the first or the second regionalisation and, by default, β equals 1. V_β has a range between 0 and 1. It equals 0 in the case of no spatial association and 1 in the case of a perfect association.

The V_measure method was applied in two main situations, namely DSMART with expert rules with original DSMART and DSMART with expert rules and DSMART with extra soil observations. The reference map is always the map derived from the DSMART algorithm with expert soil landscape relationships.

3 Results

3.1 Disaggregated soil maps

Applying DSMART-based approaches yielded a set of soil maps and associated probability of occurrence rasters. The original DSMART approach allowed for the disaggregation of the 96 SMUs into 108 STUs, while DSMART with the expert rules approach yielded 158 STUs and DSMART with the extra soil observations approach yielded 172 STUs with respect to the first most probable STU map. A total of 171 STUs were identified in the Ille-et-Vilaine region within the RRP database. Unpredicted STUs correspond mainly to rare STUs, with low proportions ranging between 2 % and 10 % within the SMUs containing them.

Figure 3 shows the three maps of the first most probable STUs derived from each approach and the original soil map. Overall, the three most probable STU maps captured the main pattern of soil distribution of the coarse soil map. As one could expect according to the geological parent material map (Lacoste et al., 2011), extensive areas of deep silty soils are developed in aeolian loam deposits encountered in the northeast and in the north-central parts of the study area. Colluvial and alluvial soils were mainly predicted in the north coast and large valley zones.

A visual comparison of the disaggregated soil maps highlighted that the global similarities in the soil spatial distribution were markedly affected by SMU boundaries. The three approaches distinguished soils developed in marsh parent material in the coastal part (north) of the study area very well. However, DSMART with the soil landscape expert rules map and DSMART with extra soil observations map remained more detailed and underlined a clear internal disaggregation of SMUs, especially in the northern and central parts of the Ille-et-Vilaine region. A visual inspection of the obtained DSMART with the extra soil observations map and DSMART with the expert rules map showed an increase in soil heterogeneity when compared to the original DSMART map. More importantly, legacy soil profiles made it possible to consider that some rare soil types with low probability would be predicted. Therefore, adding supplementary sampling points via the expert calibration data set and the 755 extra soil profiles allowed for the prediction of STUs characterised by a low spatial extent in the soil database. Nevertheless, the three DSMART-based approaches spatially disaggregated the most frequent components and disregarded the less frequent ones.

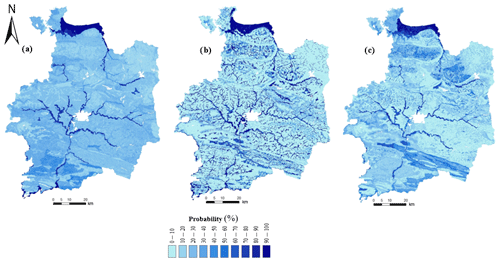
Figure 4 Global probability of hydromorphic soils over the study area derived from (a) original DSMART, (b) DSMART with soil landscape relationships and (c) DSMART with extra soil observations. The probabilities of the three STUs with the highest prediction occurrence are summed if they are hydromorphic.

Figure 4 shows maps of the global probability of redoximorphic soils across the study area. STU probability rasters, depicting hydromorphic soils, were added together to produce continuous maps of hydromorphic soil probability. A visual inspection of the three maps highlighted the global similarities, but local differences were recorded along the hydrographic network and in the southern part of the study area. As could be expected, DSMART with expert rules predicted hydromorphic soils in valleys and coastal areas well, with a probability of occurrence exceeding 80 %. Adding soil landscape relationships to the allocation process constrained the hydromorphic soil predictions in specific landscape positions. The same trend characterised DSMART with the extra soil observations map, particularly in the central part of the study area. Therefore, including 755 soil profiles had an important role in the disaggregation process in the northern and the central parts where these profiles were located.

Figure 5 Confusion index maps for the (a) original DSMART approach, (b) DSMART with expert rules and (c) DSMART with extra soil observations.

The uncertainty of the maps resulting from DSMART-based approaches was quantified via the probabilities of occurrence for each STU predicted and the confusion index maps (Fig. 5). The latter measure indicated areas where the probability of occurrence of the two most probable soil types was close. Over the study area, the average probability of occurrence for the most probable soil type achieved 0.41 for DSMART map (method 1), 0.28 for DSMART with extra soil observations maps (method 2) and 0.68 for DSMART with expert rules (method 3), respectively. Meanwhile, the average confusion index reached 0.8 for the original DSMART approach (method 1), while DSMART with extra soil observations (method 2) and DSMART with expert rules (method 3) achieved 0.9 and 0.43, respectively. Although the most probable soil classes provide plausible maps of the soil distribution, there is a significant prediction uncertainty as depicted by these measures.

In regions where disaggregated soil maps showed a low confusion index, particularly in the northwest and on the north coast areas of Ille-et-Vilaine region, high confidence in predictions was suggested. These areas were predominantly deep loamy soils or developed in alluvial and colluvium deposits.

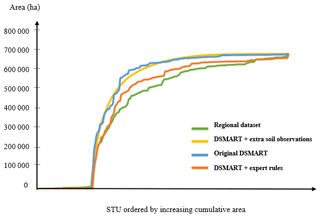
Figure 6 Cumulative area of the 171 STUs estimated from the regional soil database and predicted by different DSMART-based approaches.

Figure 6 compares the cumulative area of the STUs estimated from the three disaggregated maps and those derived from the regional soil database. For each STU, its relative predicted area was estimated by counting the number of pixels where it was predicted. For the regional soil database, each STU area was computed from the total SMU area multiplied by the proportion of the STUs. This comparison shows that some STUs were overestimated by the disaggregation approaches when comparing them to the soil database. DSMART with the extra soil observations and original approaches showed similar cumulative STU areas under the curve, whereas DSMART with expert rules had a shape similar to the regional soil database.

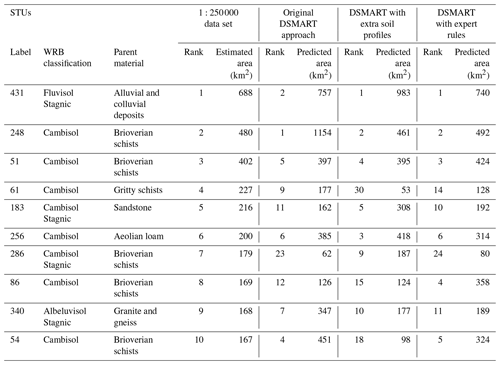
The most abundant STUs in the database (431: Stagnic Fluvisol developed from alluvial and colluvium deposits) were predicted to be the most frequent STUs by DSMART with extra soil observations and DSMART with expert rules, and it was predicted as the second most abundant STUs by the original DSMART algorithm. The 10 most abundant STUs in the soil database cover almost 43 % of the study area. Of these, seven belong to the 10 STUs most predicted by the three disaggregation approaches (Table 2).

Table 2 The 10 most extended STUs, according to the regional soil database, and their respective rank by area using three DSMART-based disaggregation procedures.

3.2 Covariates importance in the decision trees

Figure 7 gives the relative importance of the covariates used in DSMART-based approaches. Soil parent material and SMU boundaries were used systematically in the conditional rules regardless of the disaggregation method. This was consistent with the contrasting pattern of the geology and the dependence relationship between SMUs and their soil components. Considering the original DSMART approach (Fig. 7a), the distribution functions of aeolian silt deposits, the airborne gamma ray spectrometry variables (K : Th ratio) and the elevation contributions were more dispersed, according to the STUs considered, than those of other covariates. For instance, the aeolian silt deposits contribution varied between 20 % and 80 %, with a median value of 42 %, whereas the slope contribution ranged between 20 % and 40 %, with a median value of 28 %. Aeolian silt deposits are significant due to their ability to represent soils inherited from superficial parent material which is poorly represented in lithological maps.

DSMART with soil landscape relationships (Fig. 7b) showed almost the same distribution function of all the covariates, except for elevation where the distribution function was more dispersed. Since a part of the training samples was chosen with expert knowledge based on three environmental covariates, namely TPI, a waterlogging index and soil parent material, we would expect the prominent role of the waterlogging index and TPI to constrain hydromorphic soil predictions and to achieve an STU distribution in the appropriate order along the toposequence. This most likely explains the dominance of Fluvisol Stagnic in valley areas, followed by a transition to Cambisols commonly found at upslope and mid-slope positions along the toposequences.

Analogous to the original DSMART algorithm, DSMART with the extra soil observations (Fig. 7c) highlighted almost the same distribution of the use of the soil environmental covariates in the decision trees, except for aeolian silt deposits, K : Th ratio and elevation. The latter covariate contributions remained less dispersed compared to the original DSMART approach.

3.3 Validation of disaggregated soil maps

The validation procedure was performed for each DSMART-based approach applied, considering the three most probable soil types and using both the semantic objects (STUs or soil groups) and spatial neighbourhood (per pixel or 3×3 window of pixels).

Considering the 755 legacy soil profiles prospected in the framework of the Sols de Bretagne project, per pixel validation accuracy reached 27 % for original DSMART maps and 34 % for DSMART with expert rules (Table 3). A similar comparison using 135 validation sites derived from the Soilserv project showed that 18.1 % of soil profiles match DSMART maps, 19.8 % match DSMART with expert rules maps and only 16.9 % match DSMART with extra soil observations maps (Table 3). Using a 3×3 window of pixels markedly improved the global accuracy, which increased for the two validation data sets (Table 3). DSMART with soil landscape relationships remained the best-performing method.

When compared to accurate soil maps (1:25 000), the validation procedure showed that DSMART with extra soil observations and DSMART with soil landscape expert rules had almost the same performance (namely 37 % and 38 %), while the best accuracy (44%) was observed for original DSMART maps (44 %; Table 3). These scores were clearly improved by considering the soil groups and 3×3 pixels neighbourhoods. For instance, the accuracy of DSMART with the expert rules maps using the soil group reached 45.9 % and increased to 62.1 % when considering 3×3 pixels windows (Table 3).

Moreover, disaggregated soil maps were compared to soil type maps extracted from existing 1:25 000 scale soil maps using the Kappa index, which was computed based on the confusion matrix of the first most probable soil type of each soil mapping approach (namely method 1, method 2 and method 3). Overall, the Kappa index ranged from 0.43 to 0.49, which can be considered moderate. Method 3 showed a better performance with a higher Kappa index (0.49). The most accurately predicted soil types were Cambisol and Fluvisol. The Kappa index of method 1 reached 0.45, while method 1 (original DSMART algorithm) showed the worst Kappa index (0.43)

3.4 Comparing disaggregated maps

Figure 8 shows the inhomogeneity maps measured by the Shannon entropy. The map derived from DSMART with soil landscape relationships was chosen as a reference map. This map deeply disaggregates the initial SMUs into 120 653 regions with irregular shapes. By contrast, the original DSMART map remained very similar to the original map and delineated the study into 40 459 regions. Both disaggregated maps reflect the main pattern of soil distribution over the study area despite the difference in the disaggregation process. A visual inspection of the maps of DSMART with the soil landscape rules and original DSMART revealed an overall similarity between the disaggregated maps, but local differences between them were depicted.

We calculated h₁=0.49, c₁=0.58 and V₁=0.53 as the global measures of the spatial agreement between the two maps (DSMART with expert rules and original DSMART). The average homogeneity of DSMART with the soil landscape rules map with respect to the original DSMART map was qualified via the h homogeneity index. Similarly, the average homogeneity of the original DSMART map, with respect to the DSMART with soil landscape rules map, was qualified via the c completeness index. Visually, the Fig. 8b map seems to be more homogeneous than the map in Fig. 8a, which is in agreement with the statistical assessment that c>h. The large number of DSMART with soil landscape rules map regions, which was 3 times higher than original DSMART map zones, might explain this difference. It is more likely that DSMART with soil landscape rules map regions cross through multiple original DSMART map zones than vice versa. However, the two disaggregated maps remained spatially associated according to the high V₁ score. The two inhomogeneity maps (Fig. 8a–b) highlighted the locations of greatest differences between two maps, mainly along the hydrographic network.

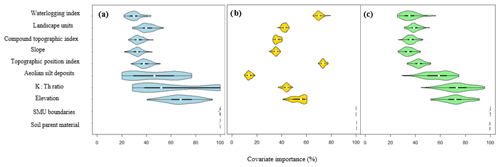
Figure 7 Violin plots of the relative importance of each environmental covariate used in the (a) original DSMART approach, (b) DSMART with expert rules and (c) DSMART with extra soil observations.

Table 3 Overall accuracies (%) obtained using various external validation approaches for the three most probable STUs.

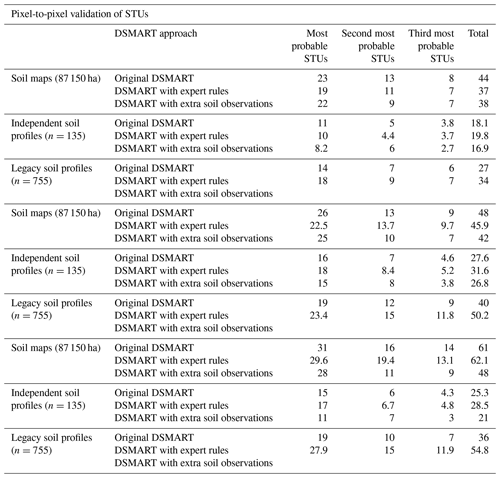
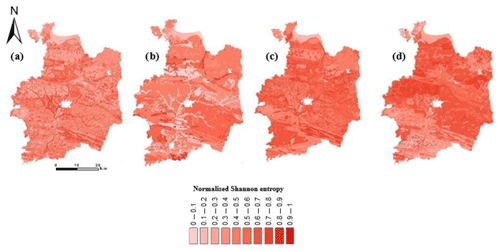
Figure 8 Spatial association between the disaggregated maps of the Ille-et-Vilaine region. (a) Map of the inhomogeneity of DSMART with the soil landscape relationship map in terms of the original DSMART map. (b) Map of the inhomogeneity of the original DSMART map in terms of DSMART with the soil landscape relationship map. (c) Map of the inhomogeneity of DSMART with soil landscape relationship map in terms of DSMART with extra soil observations map. (d) Map of the inhomogeneity of DSMART with the extra soil observations map in terms of DSMART with the soil landscape relationship map. Inhomogeneity (variance) is measured by the normalised Shannon entropy.

When comparing disaggregated soil maps derived from the modified DSMART algorithm (DSMART with soil landscape rules and DSMART with supplement soil observations), we note that DSMART with the extra soil observations map delineated the study area into 132 942 regions. For both maps, internal disaggregation was well pronounced except for DSMART with the extra soil observations map in the southern part of the study area. A visual inspection of the selected maps showed a high spatial agreement and highlighted some locations of greatest differences, particularly in the southern part of the Ille-et-Vilaine region. Even if the hydrographic network was well detailed in both maps, it appeared more developed in DSMART with the extra soil observations soil map.

Applying the V_measure method for assessing the spatial similarities between DSMART with the soil landscape rules map and DSMART with the supplement soil observations map provided similar information in terms of the theoretical measures, namely h₂=0.47, c₂=0.48 and V₂=0.47. A visual comparison of the soil inhomogeneity maps revealed a constant variance measured by the normalised Shannon entropy. This was in agreement with the quantitative assessment of c=h. Overall, the two disaggregated maps were spatially correlated, as indicated by the global spatial agreement measure V₂.

4 Discussion

4.1 Performance of the disaggregation procedures

The disaggregated soil maps produced closely resemble the abundant soils in the original soil map (Holmes et al., 2015; Fig. 3). The first most probable STU map derived from DSMART-based approaches captured the main spatial pattern of the soil distribution across the study area. More internal variation within SMUs was found when using DSMART with added point observations and DSMART with soil landscape relationships. Local soil heterogeneity reflecting the inherent pedological complexity was depicted by the first STU maps, which delivered a deterministic soil landscape distribution with continuously varying landscape features.

External validation was performed to assess the quality of the disaggregated soil maps. Using 135 independent soil profiles and a per pixel validation approach, the overall accuracy reached 18.1 % for the DSMART algorithm's first STU map, 19.8 % for DSMART with the expert rules' first STU map and 16.9 % for DSMART with the extra soil profiles' first STU map. In the DSM literature, researchers who applied classification tree decision methods found similar validation results. For instance, by applying the DSMART algorithm to eastern Australia and using 285 legacy soil profiles, Odgers et al. (2014) achieved an overall accuracy of 23 %. Similarly, Nauman and Thompson (2014) explored the use of expert rules for the soil landscape relationships in the United States of America and achieved a global accuracy ranging between 22 % and 24 %. Similar disaggregation performance was recorded by Holmes et al. (2015) in Western Australia (20 %), Chaney et al. (2016) in the United States of America (17 %) and Møller et al. (2019) in Denmark (18 %) using DSMART algorithm (Table 4). In contrast to the latter studies, a large number of STUs (171 STUs) comprise our soil data set. This could certainly decrease the chance of predicting the right STUs, despite mobilising relevant geographic data sets to implement soil landscape relationships.

Table 4 Comparison between the size areas covered, number of soil map units, soil type units of the original legacy soil maps and the accuracy achieved in other studies using DSMART algorithms.

When considering a window of 3×3 pixels, the overall accuracy increased considerably for the three DSMART-based approaches maps, but DSMART with the expert soil landscape relationships achieved the highest accuracy scores. Chaney et al. (2016) highlighted a high degree of spatial noise in the predictions by including pixel validation neighbours. Overall, prediction accuracy increased twofold with a 3×3 pixel validation window and when grouping soils to a coarser level of soil classification (171 vs. 89 soil groups). This was recorded for all disaggregated maps regardless of the disaggregation procedure and suggests that fine soil taxonomic dissimilarities cannot be accurately mapped by disaggregation processes.

4.2 Legacy soil data

Legacy soil data used in this study provide an overall representation of soil over large areas (1:250 000 scale). This database was derived from several soil surveys and pedological expert knowledge. SMUs were spatially delineated, and their spatial organisation, and STUs features, was described according to available soil data and pedological expertise. STUs and their associated landscape characteristics were identified as accurately as possible using legacy soil profiles collected according to a not probabilistic sampling design between 1968 and 2012. Hence, differences in survey methods covering a large area over a long sampling period could lead to errors in the STU definition or to uncertainties in the estimation of their area in a given SMU.

Moreover, soil survey intensity was not uniform within SMUs. Thus, SMU components may be derived from the unequal representation of soil samples across SMUs.

Harmonising soil data to reduce the number of STUs is a great challenge by itself. Grouping some STUs regarding their pedological similarities, such as sharing comparable morphological criteria, having similar pedogenic horizons and occurring in analogous environmental conditions, is worth investigating. More importantly, unifying soil data according to more functional aspects, such as soil agricultural potential, also allows for the generation of a relevant regional soil database that is easily handled by soil users to satisfy their needs. Many countries around the world have already harmonised their soil databases, such as Denmark and Australia, where high pedological complexity was captured with a reasonable STU number – not exceeding 23 soil groups in Denmark (Møller et al., 2019) and 73 soil groups in Australia (Holmes et al., 2015).

4.3 Taxonomic similarities

In the recent DSM literature, the DSMART approach is considered as an efficient tool for disaggregating existing coarse soil maps. In this study, we compared variants of the DSMART-based approach, which differed according to the training data set used to calibrate the C5.0 model and the allocation procedure. Modified DSMART algorithms used additional calibration data sets derived from supplement soil observations and expert sampling of polygons. Hence, taxonomic similarities were not considered in the calibration process nor in the current component assignment scheme. Even if there is a large number of STUs addressing the inherent soil landscape heterogeneity, there is most likely a short taxonomic distance between many of them. As a result, these STUs may have similar forming conditions, making it a challenge to suitably constrain the prediction probabilities using a DSMART algorithm. This likely explains the high confusion index scores recorded in the present study, particularly for original DSMART and DSMART with the extra soil profile approaches. As demonstrated by Minasny and McBratney (2007), including taxonomic distance in decision trees using pedological knowledge is a relevant way to decrease the misclassification error. Therefore, future efforts, and improvements in the DSMART algorithm, should take into account the taxonomic distance between STUs in the disaggregation procedure.

4.4 Mapping comparison

A quantitative comparison between the disaggregated soil maps was performed using a novel approach called the V_measure method. This method was commonly used to assess the spatial agreement between land cover maps and thematic biotic and abiotic factor maps, as done by Nowosad and Stepinski (2018) in the United States of America, but never before for soil maps.

In the present study V₁ (0.53) was larger than V₂ (0.47), suggesting that DSMART with the expert soil landscape relationship map is much more similar to original DSMART map than DSMART with the extra soil observations map. This might be explained by the allocation procedure for training samples. The original DSMART algorithm tends to promote the most abundant STUs with high proportions of occurrence within polygons and penalise STUs with low proportions (comprising between 2 % and 10 %). Therefore, frequent STUs are more likely to be predicted rather than rare STUs. Meanwhile, by adding supplementary soil profiles preliminarily assigned to a suitable STU in the training data set, we constrain STUs with low proportions of occurrence predictions.

The major differences between DSMART with the expert rules map and DSMART with the soil observations were mainly observed in the southern part of the study area and valley areas. In general, Fluvisol Stagnic soils were overestimated by DSMART with extra soil observations. This was likely due to the purposive sampling design followed to supplement the soil observations. The 755 legacy soil profiles were selected to characterise hydromorphic soil conditions and to characterise that inherent soil landscape variability that was supposed to be organised along the hill slope.

4.5 Improvements and future work

Even though this work emphasises the contribution of pedological knowledge to the disaggregation process, other pathways can also be explored to improve the map's accuracy. As recommended by Mulder et al. (2016), compensating the temporal changes and differences in laboratory analytics is a good option for improving the quality of legacy soil data. This suggests harmonising the local soil database and regrouping some STUs with similar soil-forming factors through statistical modelling. Moreover, additional environmental covariates with high spatial resolutions should be used to capture the micro-landscape variability (Lacoste et al., 2014; Odgers et al., 2014; Chaney et al., 2016; Møller et al., 2019). For example, adding a more detailed digital elevation model allowed the capturing of small terrain features where STUs occurred. Improving both the polygon sampling procedure and current components assignment scheme turned out to be important for reducing the uncertainty prediction. This suggests drawing virtual soil samples proportionally to polygon areas and using supplementary STU characteristics based on surveyor observations (namely slope shape, hill slope position, soil texture, etc.) to guide the STU allocation procedure (Møller et al., 2019). Assuming that the decision tree can be built to relate STU descriptors to legacy soil data, this method can replace the weighted random allocation procedure and should help minor STU predictions by constraining raster probabilities.

5 Conclusions

We applied three DSMART-based approaches, including the original DSMART algorithm, DSMART with the extra soil observations and DSMART with the soil landscape relationships, to disaggregate legacy soil polygons over a large area in Brittany (France). Regardless of the disaggregation approach, the produced soil maps, at a 50 m spatial resolution, successfully address the main soil spatial pattern regarding prior the pedological knowledge of our study area. Performance was assessed against 135 independent soil profiles, 755 legacy soil profiles and accurate 1:25 000 soil maps highlighted that DSMART with the expert rules maps achieved the highest validation measures. Overall, modified DSMART algorithms allowed for minor STU predictions, whereas the original DSMART algorithm promoted abundant STU predictions with poor spatial structure improvements. Adding pedological knowledge and extra soil observations to the prediction process constrained STU probabilities, even for STUs with low proportions. However, some particular STUs reflecting hydromorphic soils or loamy soils were greatly overestimated for all the three DSMART-based approaches.

Soil maps produced using the original DSMART and DSMART with the expert rules had a high spatial agreement, but the latter maps appeared more detailed and provided spatially continuous and consistent STU predictions. Therefore, generalising soil landscape relationships that take several STU descriptors and landscape features into account should be implemented in the future versions of the DSMART algorithms to capture soil landscape heterogeneity and consequently guarantee coherent variability of the soil properties.