The effect of groundwater depth on topsoil organic matter mineralization during a simulated dry summer in northwestern Europe

With climate change expected to intensify the occurrence and severity of droughts, the impacts of the groundwater table (GWT) depth and capillary rise on topsoil moisture may become critical drivers of biological activity. Consequently, the GWT depth could influence topsoil carbon (C) mineralization. In this study, undisturbed 200 cm long soil columns with three different textures (loamy sand, sandy loam and silt loam) were subjected to two artificial GWT depths (−165 and −115 cm) in the laboratory. We examined (1) upward moisture flow by capillary action along the soil profile, specifically into the top 20 cm of soil, and (2) the effect of the GWT on the decomposition of an added ¹³C-enriched substrate (ryegrass) over a period of 10 weeks, with limited wetting events representing a dry summer. A 50 cm difference in the GWT depth (−165 vs. −115 cm) resulted in different topsoil moisture values for the sandy loam (31 % vs. 38 % water-filled pore space – WFPS) and silt loam (33 % vs. 43 % WFPS) soils. In the loamy sand soil, GWT-induced moisture differences appeared only up to 85 cm above the GWT. The expected acceleration of the mineralization of the added ryegrass under a shallower GWT was not confirmed. In contrast, CO₂ efflux pulses after some of the wetting events were even higher for the drier −165 cm GWT than for the −115 cm GWT across all three soil textures. Additionally, a model fitted to cumulative ryegrass mineralization showed a lower mineralization rate for the stable C_ryegrass pool in the silt loam soil with the shallowest GWT, where capillary rise contributed most significantly to topsoil moisture, compared with other combinations of soil texture and GWT depth. These findings suggest that the upward capillary moisture flow, along with the resulting increase in topsoil moisture and the anticipated enhancement of biological activity and ryegrass mineralization, might have been counteracted by other processes. One possible explanation could be that rewetting may have triggered a stronger mineralization response, commonly known as the Birch effect, in drier topsoils compared with conditions in which the soil remained consistently wetter with a shallower GWT level. Based on our findings, inclusion of the process of texture-specific capillary supply from the GWT is required to adequately simulate moisture in the topsoil during droughts as they occurred over the past summers in northwestern Europe, depending on the GWT–texture combination. However, the net effect on topsoil C mineralization is complex and warrants further investigation, including the integration of processes related to fluctuations in soil moisture following rewetting.

1 Introduction

When soil desiccates, the soil water potential becomes strongly negative, making ecophysiological conditions less favorable for soil microorganisms. In particular, the intracellular turgor pressure and cellular integrity are no longer guaranteed (Malik and Bouskill, 2022; Wang et al., 2015), while the diffusion of substrates and extracellular enzymes becomes impeded (Manzoni et al., 2016). As a result, carbon (C) and nitrogen (N) mineralization in soils is strongly moisture dependent. Therefore, soil C models simulate moisture through hydrological modules. As precipitation and irrigation are usually the primary suppliers of topsoil moisture, most models do not account for lateral or upward moisture influxes. However, during prolonged dry periods, drying out of topsoil may lead to the establishment of counter-gravity soil suction gradients, inducing the significant upward redistribution of water from the groundwater table (GWT) to the vadose zone through capillary action and, as such, controlling topsoil moisture. With progressing climate change throughout Europe, weather patterns are becoming more erratic, and this Maritime climatic region has already been experiencing an increased occurrence of unusually lengthy dry periods and even agricultural drought over the past few years (Aalbers et al., 2023; Toreti et al., 2022).

Whether or not moisture supply via upward capillary flow is a relevant process that needs to be accounted for by soil C models will not only depend on climate but also on factors such as the depth of the GWT and soil physical properties. However, to date, the effect of the GWT depth and capillary moisture supply has nearly exclusively been studied in relation to crop yields (Awan et al., 2014; Feddes et al., 1988; Kroes et al., 2018; Zipper et al., 2015) and irrigation needs (Babajimopoulos et al., 2007; Jorenush and Sepaskhah, 2003; Prathapar et al., 1992; Yang et al., 2011). For example, Zipper et al. (2015) found optimal maize crop yields at GWT levels of 0.6, 0.8 and 0.9 m depth for sandy loam, loam and silt loam soils, respectively, and attributed this to an optimal water supply resulting from capillary action. When considering bare soils, simulations of the so-called extinction depth for GWT evaporation resulted in depths of 70, 130 and 420 cm for loamy sand, sandy loam and silt loam soils, respectively (Shah et al., 2007). This diverse range of modeling outcomes highlights the site-specific nature of capillary rise. To the best of our knowledge, no robust proof exists regarding if or when the GWT depth might significantly control topsoil heterotrophic activity. Such insights are essential to determine whether the incorporation of the GWT depth and upward capillary moisture flow in updated soil C models is warranted. To validate simulation results, a few studies have been carried out using parallel small-scale field lysimeter experiments monitoring the soil water balance (Kelleners et al., 2005; Prathapar et al., 1992; Yang et al., 2011). Alternatively, Grünberger et al. (2011) injected a deuterium-enriched solution into the GWT to follow capillary rise in arid areas. However, both approaches are labor-intensive and/or require large monetary investments and high levels of technical expertise. In contrast, Li et al. (2022) simply excluded upward capillary moisture transport in a field trial on crop residue decomposition by placing a 5 cm gravel layer at a depth of 50 cm. They found that, for sandy soils, a GWT depth of just 60 cm was not shallow enough to notably provide the top 25 cm of soil with capillary moisture. However, this approach required the disturbance of the topsoil; moreover, the artificial break in capillary rise also unintentionally canceled out unsaturated downward water redistribution. Most importantly, perhaps, the main impediment of observational field approaches, such as those listed above, is their inability to control ambient factors such as the GWT depth, precipitation, temperature and relative humidity. This limitation restricts our ability to study the effect of individual components of the soil water balance, like the capillary moisture supply.

As an alternative, a handful of laboratory-scale experiments have sought to infer the capillary moisture impact on soil biogeochemical processes. Rezanezhad et al. (2014) and Fiola et al. (2020) reported that the highest C mineralization was found under transient redox conditions above the capillary fringe, where moisture and oxygen are in balance. However, due to the small scale of the setups used (packed-soil columns of 45 and 30 cm length in the respective aforementioned works), an appreciation of capillary rise was not possible. Malik et al. (1989), Shaw and Smith (1927), and Lane and Washburn (1947) assembled larger packed-soil columns to determine the maximum capillary rise height as a function of soil texture. They found a capillary moisture supply up to 149 cm (loamy sand soil), 183 cm (sandy loam soil) and 359.2 cm (silt soil). However, as those columns were repacked from sieved soil, the soil structure was disrupted and the in-field heterogeneity and macropores were not well represented (Lewis and Sjöstrom, 2010); moreover, the impact on C mineralization was not assessed. In summary, there is little empirical evidence of the control of moisture dynamics by capillary water flow on topsoil organic matter (OM) mineralization. Not only does the impact of the GWT on mean topsoil water content seem to be a blind spot, but the amplitude of soil moisture fluctuation in topsoil may also possibly depend on the magnitude of the moisture supply via capillary action. After a rainfall event, the rewetting of dry soil leads to strongly increased C mineralization, often referred to as the Birch effect (Birch, 1958). This effect depends on the magnitude of the soil moisture increment and/or drier pre-wetting conditions (Liang et al., 2023). With a stronger continuous supply of moisture via capillary rise, we may expect smaller fluctuations in topsoil moisture as well as smaller Birch-effect-induced soil C mineralization peaks.

Our main aim was to study if, during a (simulated) period with limited rainfall, there would be a significant effect of capillary moisture flow from the GWT on topsoil moisture and OM mineralization for arable lands comprised of loess deposits in northwestern Europe. We designed a setup wherein excavated 200 cm long undisturbed soil columns were incubated in the laboratory, with ambient factors being regulated and soil moisture being monitored. Columns of three soil textures were subjected to minimal watering events representing a dry summer, and two GWT depths were utilized to study the interaction between both factors and to provide a representative depiction of our study region, i.e., northwestern Europe. The decomposition of an introduced substrate, i.e., ¹³C-enriched ryegrass, was monitored using CO₂ headspace measurements. We hypothesized that a deeper GWT would result in reduced topsoil moisture and that, as a result, C mineralization in the topsoil would be relatively inhibited compared with the treatment with shallower GWT. We expected an increasing susceptibility to reduced moisture of the C mineralization with a coarser soil texture, as water losses by evaporation would be less compensated by capillary moisture input. Although physicochemical protection of OM is stronger in finer-textured soils, we expected that such a direct effect of soil texture on the mineralization of the added OM would be of less importance in the short term (10 weeks) compared with the regulation of soil moisture by the soil texture–GWT depth combinations.

2 Material and methods

2.1 Study area and undisturbed soil column collection

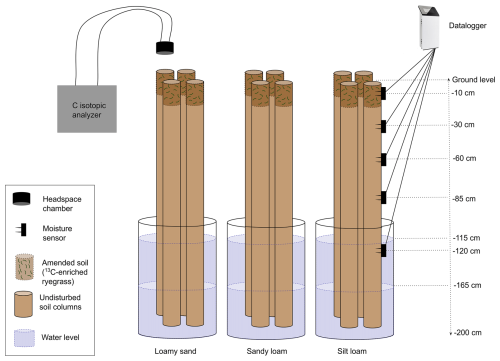
Undisturbed soil columns were collected from three croplands in northwestern Belgium with different soil textures: a loamy sand soil ($\mathrm{50}\mathit{°}{\mathrm{55}}^{\prime }{\mathrm{43.8}}^{\prime \prime }$ N, $\mathrm{3}\mathit{°}{\mathrm{32}}^{\prime }{\mathrm{54.7}}^{\prime \prime }$ E; Kruisem), a sandy loam soil ($\mathrm{50}\mathit{°}{\mathrm{57}}^{\prime }{\mathrm{47.3}}^{\prime \prime }$ N, $\mathrm{3}\mathit{°}{\mathrm{45}}^{\prime }{\mathrm{37.2}}^{\prime \prime }$ E; Bottelare) and a silt loam soil ($\mathrm{50}\mathit{°}{\mathrm{55}}^{\prime }{\mathrm{15.8}}^{\prime \prime }$ N, $\mathrm{3}\mathit{°}{\mathrm{45}}^{\prime }{\mathrm{03.0}}^{\prime \prime }$ E; Oosterzele). According to the World Reference Base for Soil Resources (WRB) soil classification map of Flanders (Dondeyne et al., 2014), the soil profiles originating from Kruisem and Bottelare are classified as Eutric Retisols, whereas the soil profiles from Oosterzele are Eutric Cambisols (Siltic). The fields were chosen based on their GWT depths of between 100 and 200 cm in the year prior to our experiment. A cylinder auger set and a motorized percussion hammer (Eijkelkamp, the Netherlands) were employed to excavate the soil columns (∅: 9.7 cm). First, 100 cm long columns were taken from the soil surface down to −100 cm depth. Second, a 100 cm deep pit (2 m²) was dug to likewise collect columns from −100 to −200 cm depth within the pit. Additionally, disturbed topsoil samples (from 0 to −20 cm) were collected near each sampling location. The soil columns were carefully transferred into PVC liners (two pipe halves tied together by strong cable ties) and transported to the laboratory. The two soil columns taken within one soil profile were then combined in 200 cm long PVC tubes that were cut lengthwise beforehand to enable the transfer and later sensor installation. On the inner walls of the PVC tubes, a waterproof foil was applied to avoid moisture losses. To ensure a hydrological connection between the two 100 cm samples, 5 cm of silt clay loam soil (17 % sand, 48 % silt and 35 % clay) was added in between. Additionally, small breaks were restored using this soil; however, when confronted with larger amounts of damage, cores were discarded. Therefore, for each field and depth increment, six columns were deliberately sampled, although only the four best, structurally intact replicates were retained for our experiment. After closing the PVC tubes, cable ties were tightly applied to attain a solid setup and avoid sidewall effects (Lewis and Sjöstrom, 2010).

2.2 Experimental design

2.2.1 Laboratory setup and incubation

A soil incubation experiment was set up in which mineralization of a model ¹³C-labeled substrate amended to the topsoil was followed as a function of two constant GWT depths (relative to the soil surface): −165 and −115 cm (Fig. 1). The top 20 cm of the soil columns was removed, such that undisturbed columns of 180 cm length remained. The GWT treatments were consecutively applied to the same columns, resulting in two incubation periods under similar laboratory conditions but with a renewed 20 cm of topsoil on the top of undisturbed columns. The setup was installed in a temperature-controlled (20.8 ± 0.7 °C for GWT −165 cm and 20.8 ± 1.5 °C for GWT −115 cm) dark room. The soil columns were submerged in tap water in 220 L barrels to a height of 35 or 85 cm, representing the −165 or −115 cm GWT depth, respectively. The soil columns were allowed to stabilize for 27 d. The loamy sand columns were covered with PARAFILM after 16 d to avoid further drying out. After this stabilization period, the disturbed topsoil samples (0 to −20 cm) collected near each sampling location in the field were mixed with ¹³C-enriched ryegrass and repacked to a 20 cm layer on top of the undisturbed soil columns, as described in more detail below. For both GWT treatments, the columns followed these identical preparation steps. We deliberately handled the deepest (−165 cm) GWT treatment first. This approach ensured that any potential impact of upward moisture transport on the soil structure was confined to a height above the GWT, which was then exceeded during the subsequent, shallower (−115 cm) GWT treatment.

Figure 1 Schematic overview of the laboratory setup.

We used a model OM substrate (i.e., ¹³C-labeled clipped ryegrass) and focused solely on the mineralization of this added substrate in the topsoil, without including data on native soil OM mineralization. This approach was chosen primarily because the inherently different quality and quantity of the three soils did not allow for study of the effect of GWT depth, soil texture or their interaction on soil OM mineralization. Additionally, CO₂ effluxes from the native soil OM included contributions from mineralization in the undisturbed subsoil column (from −20 to −200 cm), which remained unchanged between GWT treatment batches to reduce potential soil heterogeneity influences on moisture dynamics. As native soil OM in this subsoil had, thus, already undergone partial mineralization during the first GWT treatment, starting conditions differed for the second GWT treatment. This is particularly notable because the subsoil conditions were also kept uniform at 20 °C, which deviates strongly from expected conditions in the field, where the temperature is lower and typically decreases with depth. This discrepancy further limits the applicability of our setup with respect to assessing subsoil OM mineralization.

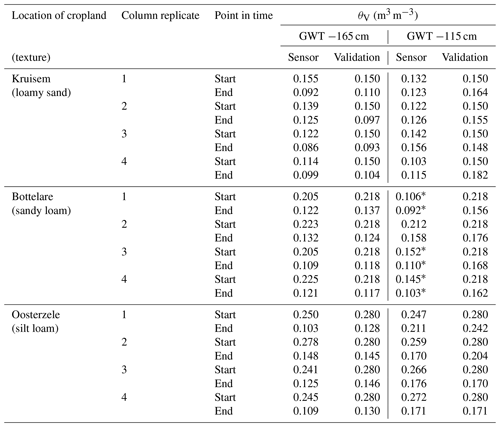
The extra, disturbed top 20 cm of soil was first dried and sieved (using a 4 mm sieve), with visible root fragments manually removed. Subsequently, the three soils were preincubated for 1 week at 20.8 °C at a water content of 0.15, 0.22 and 0.28 m³ m⁻³ for the loamy sand, sandy loam and silt loam columns, respectively. The model substrate, i.e.,  ¹³C-labeled ryegrass ($\mathit{\delta }{}^{\mathrm{13}}\mathrm{C}=+\mathrm{44.93}$ ‰ ± 1.65 ‰), was added at a dose of 1.5 g C per kilogram of dry soil (C_ryegrass=38.74 % ± 0.99 %; $\mathrm{C}:\mathrm{N}=\mathrm{12.8}$) and mixed thoroughly. The production of this ¹³C-enriched ryegrass is described by Li et al. (2023). To exclude differences in N availability between the various soil texture–GWT depth treatment combinations, KNO₃ (dissolved in water) was added at a dose equivalent to 100 kg N ha⁻¹. Each of these soil–grass mixtures for the three soil textures was then gently packed on top of the columns to bulk densities of 1.50, 1.45 and 1.40 g cm⁻³ for the loamy sand, sandy loam and silt loam columns, respectively. Volumetric water sensors (type EC-5, 5TM, TEROS 10 and TEROS 12; Decagon and METER group, USA) were installed at different depths (−10, −30, −60, −85 and −120 cm) by puncturing the sensor rods through the waterproof foil. Prior to use, all sensors were calibrated for the three specific soil textures. Dataloggers (type ZL6; METER group, USA) were used with a log frequency of 1 h. Rainfall was simulated by gently adding 85 or 128 mL over a 30 min period every 14 to 21 d, equivalent to a dose of 25 mm per month. With this watering scheme, we simulated a drier-than-usual (78 mm per month; 30-year Belgian average between 21 June and 20 September over the 1991–2020 period) local Maritime climate summer, without exceeding the actual measured lowest extreme of 5.2 mm per month only observed in July 2022 (Royal Meteorological Institute, 2022). Moisture measurements at −10 cm depth were considered to be representative of the entire repacked topsoil layer (0 to −20 cm) and, therefore, suitable for assessing ¹³C-labeled ryegrass mineralization within this layer. Simulations in HYDRUS-1D confirmed that moisture had infiltrated to a depth of approximately 20–30 cm and that, within 24–36 h after water addition, the water content had become nearly uniform throughout the 0–20 cm layer (Fig. A1 in Appendix A). As soil CO₂ efflux measurements were not taken earlier than 24–36 h after watering events, the −10 cm measurements provided a representative state of the topsoil moisture. Water levels in the barrels were kept constant daily, with the help of a float and a time-of-flight sensor (VL53L0X; Adafruit) combined with a Raspberry Pi (small single-board computer). A plastic grid with a mesh size of 5 mm placed between the undisturbed soil column and the repacked topsoil allowed removal of the topsoil after the completion of the first incubation batch while also preserving the structure and hydraulic contact with the undisturbed columns underneath. Similarly, for the second GWT treatment, fresh topsoil mixed with ryegrass was once again added. At the end of each GWT treatment incubation batch, the packed topsoil was removed and its gravimetric water content was determined. Both the initial and final gravimetric water contents were converted into the volumetric water content (θ_V), using the applied bulk densities, and compared with the sensor values (Table A1 in Appendix A). Deviating measurements were found for three sandy loam columns during the −115 cm GWT treatment, presumably due to air entrapment around the sensor rods after installation. To rectify this discrepancy, a correction was applied using linear regression (Fig. A2).

2.2.2 Soil CO₂ efflux measurements and calculations

Soil CO₂ efflux was regularly measured to record soil C mineralization and infer the progress of the cumulative amount of C_ryegrass mineralized over time. For CO₂ efflux measurements, a G2201-i cavity ring-down spectrometer (CRDS; Picarro, USA) was consecutively connected via tubing to an airtight lid attached on top of the soil columns. The lid contained two sampling ports (gas in- and outlet); a vent tube (∅: 1 mm) to minimize air pressure differences; and a 9 V battery-powered fan on the inside to ensure air circulation inside the headspace between the soil surface, PVC tube and lid. The headspace volume varied between 0.52 and 0.82 L and covered an area of 73.90 cm². The CRDS recorded changes in the headspace CO₂ concentration and δ¹³C value every 2–3 s. CO₂ efflux rates were calculated as the slope of the linearly increasing CO₂ concentration over a 7–15 min time interval per soil column and were converted to a mass-based unit ($\mathrm{mg}{\mathrm{CO}}_{\mathrm{2}}\cdot \mathrm{C}\mathrm{kg}{\mathrm{soil}}^{-\mathrm{1}}{\mathrm{h}}^{-\mathrm{1}}$) using the ideal gas law. To determine the δ¹³C (‰) value of emitted CO₂ (δ¹³C ⋅ CO₂; Eq. 1), the Keeling plot method was applied: measured δ¹³C values were plotted against the inverse CO₂ emission concentrations, and the δ¹³C of emitted CO₂ was obtained from the y-axis intercept of a linear model fitted to the data (Keeling, 1958). Measurements were made on days 1, 2, 3, 5, 7, 9, 11, 13, 15, 20, 22, 24, 27, 29, 34, 36, 38, 42, 45, 48, 52, 57, 59, 62, 66 and 69 for each of the incubation batches. The CRDS was recalibrated at the onset of each incubation using two certified standard gases of 400 and 2500 ppm CO₂ with δ¹³C values of −8.6 ‰ and −51 ‰, respectively. The contrasting δ¹³C values of the added ¹³C-labeled ryegrass (+44.93 ‰ ± 1.65 ‰) and soil organic carbon (−25.68 % ± 0.23 % for loamy sand, −25.57 % ± 0.17 % for sandy loam and −24.79 ‰ ± 0.11 ‰ for silt loam soils; Table 1) allowed one to partition the total CO₂ efflux (CO₂ ⋅ C_total) into a share resulting from ryegrass decomposition (CO₂ ⋅ C_ryegrass) and from native soil organic carbon (SOC) (CO₂ ⋅ C_SOC) (µg CO₂-C per kilogram of soil), using an isotope mixing model following Eq. (1):

$$\begin{array}{}\text{(1)}& {\displaystyle }\begin{array}{rl}{\displaystyle }{\mathrm{CO}}_{\mathrm{2}}\cdot C_{\text{ryegrass}}=& {\displaystyle \frac{\mathit{\delta }{}^{\mathrm{13}}\mathrm{C}\cdot {\mathrm{CO}}_{\mathrm{2}}-\mathit{\delta }{}^{\mathrm{13}}\mathrm{C}\cdot {\mathrm{CO}}_{\mathrm{2}\cdot \text{SOC}}}{\mathit{\delta }{}^{\mathrm{13}}\mathrm{C}\cdot {\mathrm{CO}}_{\mathrm{2}\cdot \text{ryegrass}}-\mathit{\delta }{}^{\mathrm{13}}\mathrm{C}\cdot {\mathrm{CO}}_{\mathrm{2}\cdot \text{SOC}}}}\\ {\displaystyle }& {\displaystyle }\cdot {\mathrm{CO}}_{\mathrm{2}}\cdot C_{\text{total}}.\end{array}\end{array}$$

The isotopic signature of CO₂ emitted from either end-member, i.e., $\mathit{\delta }{}^{\mathrm{13}}\mathrm{C}\cdot {\mathrm{CO}}_{\mathrm{2}\cdot \text{ryegrass}}$ or $\mathit{\delta }{}^{\mathrm{13}}\mathrm{C}\cdot {\mathrm{CO}}_{\mathrm{2}\cdot \text{SOC}}$, was analyzed in ancillary soil incubations, as in Mendoza et al. (2025). The $\mathit{\delta }{}^{\mathrm{13}}\mathrm{C}\cdot {\mathrm{CO}}_{\mathrm{2}\cdot \text{SOC}}$ was determined in parallel 20 cm packed-soil columns with no ryegrass added. For $\mathit{\delta }{}^{\mathrm{13}}\mathrm{C}\cdot {\mathrm{CO}}_{\mathrm{2}\cdot \text{ryegrass}}$, such soil columns were amended with a high dose of ryegrass (3 g C per kilogram of soil; indicated as “high”). The rationale for using smaller columns compared with the main experimental setup was to exclude CO₂ emissions from the underlying soil organic carbon (OC), ensuring a more accurate assessment of $\mathit{\delta }{}^{\mathrm{13}}\mathrm{C}\cdot {\mathrm{CO}}_{\mathrm{2}\cdot \text{ryegrass}}$. The following Eq. (2) was applied:

$$\begin{array}{ll}\text{(2)}& {\displaystyle }\mathit{\delta }& {\displaystyle }{}^{\mathrm{13}}\mathrm{C}\cdot {\mathrm{CO}}_{\mathrm{2}\cdot \text{ryegrass}}={\displaystyle }& {\displaystyle \frac{{\mathrm{CO}}_{\mathrm{2}}\cdot C_{\text{high}}\cdot \mathit{\delta }{}^{\mathrm{13}}\mathrm{C}\cdot {\mathrm{CO}}_{\text{2\hspace{0.17em}high}}-{\mathrm{CO}}_{\mathrm{2}\cdot \text{SOC}}\cdot C_{\text{SOC}}\cdot \mathit{\delta }{}^{\mathrm{13}}\mathrm{C}\cdot {\mathrm{CO}}_{\mathrm{2}\text{SOC}}}{{\mathrm{CO}}_{\mathrm{2}}\cdot C_{\text{high}}-{\mathrm{CO}}_{\mathrm{2}}\cdot C_{\text{SOC}}}}.\end{array}$$

Emission measurements in these ancillary incubations were made on days 2, 7, 15, 29 and 52.

Table 1 Physicochemical properties of the undisturbed soil columns (n=4).

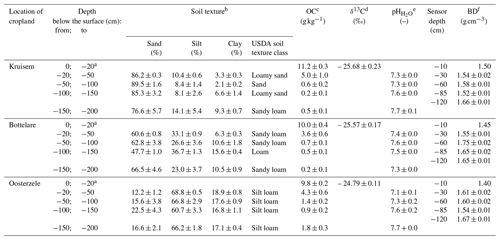
^a Repacked soil layer. ^b Measured with the pipette-sedimentation method for the following fractions: sand (0.05–2 mm), silt (0.002–0.05 mm) and clay (<0.002 mm). ^c Organic carbon (OC) measured using a FORMACS™ HT-i TOC/TN analyzer (Skalar, the Netherlands). ^d Measured with a PDZ Europa ANCA-GSL elemental analyzer interfaced with a Sercon 20-22 IRMS with SysCon electronics (SerCon, UK) and EA-IRMS EA IsoLink interfaced through a ConFlo IV to a DELTA Q (Thermo Scientific, Germany). All δ¹³C values are ${}^{\mathrm{13}}\mathrm{C}{/}^{\mathrm{12}}\mathrm{C}$ ratios expressed relative to the international VPDB (Vienna Pee Dee Belemnite) standard. ^e pH in 1:5 soil : water (volume fraction) suspensions, measured using a glass electrode. ^f BD denotes bulk density.

From the ryegrass-derived CO₂ efflux (CO₂ ⋅ C_ryegrass h⁻¹), cumulative amounts of mineralized C_ryegrass (in µg C per kilogram of soil) were calculated by integrating these mineralization rates over time intervals defined as half of the period before the previous measurement and half of the period until the next measurement. To describe the kinetics of mineralized ryegrass over time, relative to the added amount of ryegrass in percentage of C_ryegrass, the following parallel two-rate first-order kinetic model was used (Sleutel et al., 2005; Zacháry et al., 2018), Eq. (3):

$$\begin{array}{}\text{(3)}& \text{Cumulative }{C}_{\text{ryegrass}}\text{-min}\left(t\right)=C_f\cdot (\mathrm{1}-e^{-k_f\cdot t})+k_s\cdot t,\end{array}$$

where C_f (percentage of C_ryegrass) and k_f (per day) are parameters representing the easily mineralizable C_ryegrass pool and the mineralization rate, respectively, while k_s (percentage of C_ryegrass per day) is the mineralization rate constant of a more stable C_ryegrass pool.

2.3 Column analyses: physicochemical soil properties

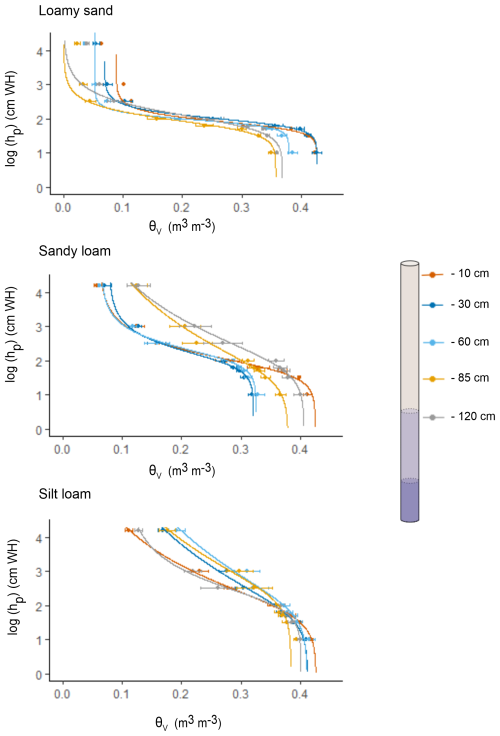
At the end of the experiment, the 200 cm tubes were opened carefully by relieving the cable ties, taking off one of the PVC pipe halves and opening the waterproof foil. Then, undisturbed soil samples (∅: 5 cm; h: 5.1 cm) were taken by pressing Kopecky rings into the soil columns near the moisture sensor locations, i.e., at −15 to −10 cm, −35 to −30 cm, −55 to −50 cm, −85 to −80 cm and −125 to −120 cm depth. For each depth layer, a soil water retention curve was determined by measuring the water contents of these ring samples on a silica sand tension table and pressure plates (Eijkelkamp, the Netherlands) at different matric tensions (−1, −3, −7, −10, −33, −100 and −1500 kPa). Average water retention curves per texture and depth (Fig. B1) were further used to convert the measured mean volumetric water contents into matric potentials, expressed as the matric head in units of centimeters of water height (cm WH). The latter values were used to calculate the hydraulic head differences (ΔH) between two measurement heights, where height was defined as increasing in the upward direction and where the hydraulic head was the sum of the matric head and gravitational head. These values were used as an indicator of the water flux direction: positive ΔH values indicated a net upward (capillary) water flux, whereas negative ΔH values signified an overall downward water flux. Soil texture, OC content and pH${}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ were determined on homogenized subsamples from the −20 to −50 cm, −50 to −100 cm, −100 to −150 cm and −150 to −200 cm layers. Values for δ¹³C were only determined for the repacked topsoil. Physicochemical properties of the soil columns are listed in Table 1.

2.4 Statistical analyses

Statistical analyses were carried out using the RStudio statistical software (version 4.1.2; R Core Team, 2021). Reported values represent means ± standard errors. Linear mixed-effect models (“lme” function in the “nlme” R package) (Pinheiro and Bates, 2000) in combination with estimated marginal means (“emmeans” function in the “emmeans” R package) (Lenth et al., 2024) were used to detect statistical differences in the average water content and C_ryegrass mineralization rates between GWT treatments per texture over the entire incubation period. In this model, the GWT treatment was set as a fixed factor, whereas column replicates (n=4) were added as a random intercept to represent the grouped structure of the experimental setup, and an autocorrelation factor was included to account for temporal autocorrelation between measurements (Schielzeth and Nakagawa, 2013). Diagnostic plots for the linear mixed-effects fit were visually examined (“plot.lme” function in the nlme R package). Additionally, paired two-tailed t tests were used to compare C_ryegrass mineralization rates between GWT treatments per measurement day (after checking assumptions of normality and homoscedasticity). The goodness of fit of the parallel two-rate first-order kinetic model was assessed using the Nash–Sutcliffe model efficiency coefficient (NSE) (“vnse” function in the “ie2misc” R package) (Embry et al., 2023). To detect any effect of GWT treatment and texture on the kinetic parameters of the two-rate first-order C mineralization model (C_f, k_f and k_s) and cumulative C_ryegrass-min at the end of the incubation, linear mixed-effect models (“lmer” function in the “lme4” R package) (Bates et al., 2015) were once more applied in combination with estimated marginal means (emmeans function in the emmeans R package). This time, both GWT and texture were set as fixed factors, whereas the separate columns (n=12) were set as a random effect to allow for a pairwise comparison. The normality assumption for the residuals was tested using a simulation-based approach (“DHARMa” R package) (Hartig, 2020).

3 Results

3.1 Soil moisture dynamics in response to GWT treatment

3.1.1 Volumetric water content (θ_V) along soil profiles of undisturbed columns

Overall, there was a gradual decrease in θ_V with increasing height above the GWT for all GWT and soil texture treatments (Fig. 2). The applied water appeared to primarily affect θ_V in the upper 10 cm but not in the deeper soil layers.

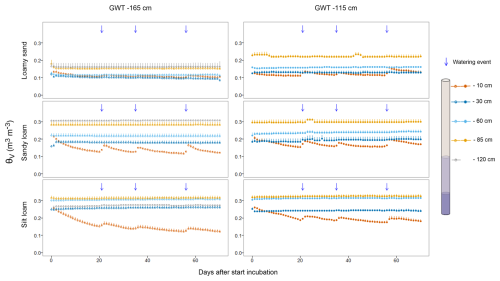
Figure 2 Evolution of soil moisture (θ_V) depth profiles (n=4) over time for two GWT (groundwater table) treatments (depths at −165 and −115 cm) and three textures (loamy sand, sandy loam and silt loam). Note that GWT treatment −115 cm does not have a sensor installed at −120 cm depth (i.e., below the established GWT).

In the loamy sand columns, moisture levels at −85 and −60 cm depth were on average 0.07 and 0.04 m³ m⁻³ lower (P=0.016 and P=0.007, respectively) for GWT −165 cm than for GWT −115 cm (Table 2). At −30 cm, a less significant (P=0.067) difference of 0.03 m³ m⁻³ was observed, while the GWT treatment did not significantly impact θ_V at −10 cm (P=0.294). The θ_V at an equivalent height of about 80 cm above both GWTs was lower for the −115 cm GWT treatment at −30 cm compared with that at −85 cm for the −165 cm GWT treatment, which was probably the result of evaporative losses. Conversely, for the −165 cm GWT treatment, θ_V was comparable at −30 and −10 cm; this might indicate a limited impact of evaporative losses on topsoil moisture.

Table 2 Estimated marginal means of water contents (θ_V) measured at different depths as a function of GWT treatment (depths at −165 and −115 cm).

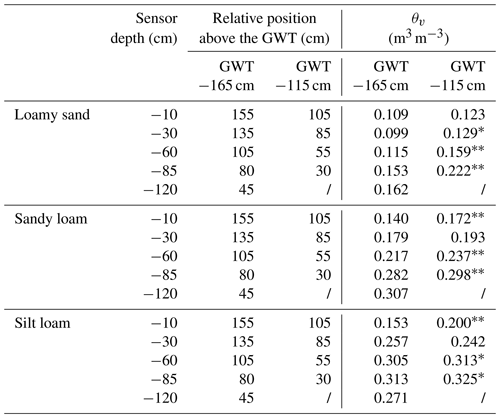
The symbols “^∗” and “${}^{\ast \ast }$” indicate that moisture was significantly higher (P<0.1 and P<0.05, respectively) for GWT treatment −115 cm when compared with the deeper −165 cm treatment. Note that GWT treatment −115 cm did not have a sensor installed at −120 cm depth (i.e., under the established GWT).

In the sandy loam columns, θ_V generally decreased with increasing height above the GWT, aside from lower θ_V at 55 cm above the −115 cm GWT (0.237 m³ m⁻³) compared with that at 80 cm above the −165 cm GWT (0.282 m³ m⁻³). This inconsistency might be explained by the elevated bulk density at −60 cm (1.75 ± 0.02 g cm⁻³) compared with that at −85 cm (1.65 ± 0.02 g cm⁻³) (Table 1). The θ_V differed significantly between both GWT treatments, with an effect of 0.02 m³ m⁻³ (P=0.012) at −85 cm, 0.02 m³ m⁻³ at −60 cm (P=0.028) and 0.03 m³ m⁻³ at −10 cm (P=0.026), but, surprisingly, not at −30 cm (0.01 m³ m⁻³, P=0.31) (Table 2).

In the silt loam columns, θ_V was comparable (about 0.310 m³ m⁻³) at depths below 30 cm from the surface (Table 2). The surprisingly lower θ_V at −120 cm (0.270 m³ m⁻³) for the −165 cm GWT treatment might again be explained by the relatively higher bulk density (1.67 ± 0.01 g cm⁻³) at that depth (Table 1). Between the GWT treatments, there were only marginally significant differences in θ_V at −85 cm (0.01 m³ m⁻³, P=0.062) and −60 cm (0.01 m³ m⁻³, P=0.092) but not at −30 cm (P=0.160). At −10 cm, θ_V was lower at GWT −165 cm (0.153 m³ m⁻³) than at GWT −115 cm (0.200 m³ m⁻³) (P=0.028).

3.1.2 Hydraulic head differences

Across all three textures and both GWT treatments, there was a negative hydraulic head difference (ΔH) between −10 and −30 cm during the first few days of the incubation. This indicates gravitational water transport (due to wetter repacked topsoil layers at the start of the experiment) towards the drier, undisturbed soil layers. In the loamy sand columns, the ΔH between −10 and −30 cm remained mostly negative for the −165 cm GWT treatment during the rest of the experiment (Fig. 3). In contrast, between −60 and −30 cm, ΔH ranged from +50 to +198 cm WH, indicating upward water movement. For the shallower −115 cm GWT, water transport between −30 and −10 cm initially occurred in an upward direction, with a maximum ΔH of +30 cm WH. However, after water application, the flow direction shifted downward, reaching a minimum ΔH of −80 cm WH. Between −60 and −30 cm, a slight positive and relatively constant ΔH (+50 cm WH) was observed. For both GWT treatments, ΔH between −85 and −60 cm remained slightly positive throughout the experimental period. Between −120 and −85 cm, we found an unforeseen negative ΔH of $\sim -\mathrm{95}$ cm WH.

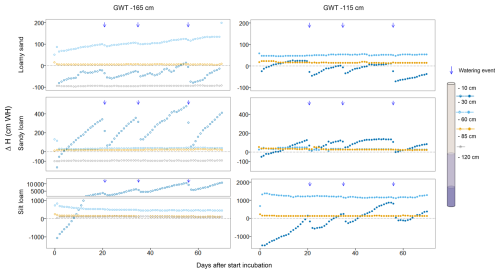
Figure 3 Difference in hydraulic head (ΔH) over time for both GWT treatments (−165 and −115 cm) measured in loamy sand, sandy loam and silt loam soil columns. A positive (negative) ΔH indicates a hydraulic head difference enabling upward (downward) moisture transport. Note that GWT treatment −115 cm did not have a sensor installed at −120 cm depth; therefore, no ΔH can be shown for −85 cm.

In the sandy loam columns, ΔH was positive between −30 and −10 cm and fluctuated in response to water application for both GWT treatments. In the −165 cm GWT treatment, higher ΔH maxima were observed as a result of drier topsoil compared with the −115 cm GWT treatment. Both GWT treatments exhibited fairly consistent positive ΔH between −60 and −30 cm as well as between −85 and −60 cm, with average ΔH values of $\sim +\mathrm{37}$ and $\sim +\mathrm{20}$ cm WH (GWT −165 cm) and of $\sim +\mathrm{32}$ and $\sim +\mathrm{29}$ cm WH (GWT −115 cm). Surprisingly, as for the loamy sand columns, we measured a negative ΔH of about −95 cm WH between −120 and −85 cm for the GWT −165 cm treatment, i.e., close to the GWT.

In the silt loam columns, ΔH in the topsoil increased up to +10 800 cm WH for the −165 cm GWT treatment as a result of the topsoil drying out compared with the underlying soil. For the shallower GWT of −115 cm, the ΔH between −10 and −30 cm fluctuated around 0 cm WH, with temporary negative values (i.e., downward moisture transport) directly after watering events followed by an increase in ΔH to positive values after several days (i.e., upward moisture transport). For GWT −165 cm, positive ΔH values were found in all subsoil layers, which tended to decrease over time from +830 to +450 cm WH, from +245 to +100 cm WH, and from +120 to +30 cm WH between respective depths of −60 to −30 cm, −85 to −60 cm and −120 to −85 cm. For the −115 cm GWT, upward (but rather constant) moisture transport existed as well, with average ΔH values of +1200 and +135 cm WH for −60 to −30 cm and −85 to −60 cm, respectively.

3.2 Mineralization of added ryegrass

3.2.1 Mineralization rates and moisture in topsoil

During the initial 5 d of the incubation, ryegrass mineralization rates were highest, with mean maxima of 1643, 1053 and 1133 µg C_ryegrass per kilogram of soil per hour for loamy sand, sandy loam and silt loam columns, respectively. From day 7 onwards, the rates decreased gradually over time; after day 30, rates averaged around 72, 62 and 78 µg C_ryegrass per kilogram of soil per hour for the three respective aforementioned textures (Fig. 4). There was no significant effect of GWT treatment on the mean C_ryegrass mineralization rate across the entire incubation period per texture, although rates did alternate between the GWT treatments for some individual measurement days. After the water application, mineralization rates in the drier (−165 cm GWT treatment) soil seemed to be more sensitive to moisture input. Significant differences were observed only in comparison to the −115 cm GWT from the second watering application onwards in the loamy sand soil (72 vs. 51 µg C_ryegrass per kilogram of soil per hour at day 36), and after the third application for the sandy loam (59 vs. 32 µg C_ryegrass per kilogram of soil per hour at day 59) and silt loam (51 vs. 13 µg C_ryegrass per kilogram of soil per hour at day 57) soil.

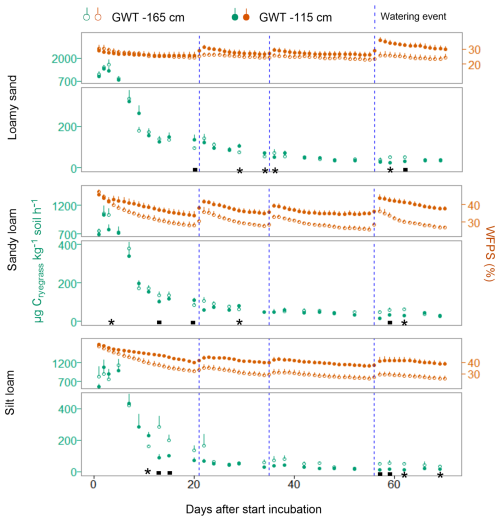
Figure 4 Ryegrass mineralization rates combined with the topsoil moisture expressed as the percentage of water-filled pore space (WFPS) for both GWT treatments in the loamy sand, sandy loam and silt loam soil columns (n=4). The symbols “▪” and “*” indicate significant differences for a specific measurement day at P<0.1 and P<0.05, respectively.

3.2.2 Cumulative ryegrass mineralization

Overall, 15 %–20 % of the added C_ryegrass was mineralized over the course of the 70 d incubation period. Cumulative C_ryegrass-min did not differ between the three soil textures (19.3 %, 15.7 % and 17.4 % for the loamy sand, sandy loam and silt loam, respectively). In contrast, GWT treatment had a marginal significant effect (P=0.051), with lower cumulative C_ryegrass-min for the −115 cm GWT (16.2 %) compared with the −165 cm GWT (18.7 %).

The kinetic parallel two-rate first-order mineralization model fitted very closely to the cumulative C_ryegrass-min, with NSE values >0.98 (Fig. 5). The estimated size of the easily mineralizable pool (C_f) was not different between the texture–GWT depth combinations, with average values between 10.3 % and 15.0 % of the initially added amount of C_ryegrass (Table 3). The mineralization rate of this fast C_ryegrass pool (k_f) was not different between the GWT treatments, but it was 0.041 and 0.026 d⁻¹ lower for the silt loam compared to the loamy sand (P=0.004) and sandy loam (P=0.049) soils, respectively. After the depletion of the fast C_ryegrass pool in about 2–3 weeks, the cumulative C_ryegrass-min further proceeded at a much slower pace following a close-to-linear course, described by k_s. This k_s was significantly lower for the −115 cm GWT silt loam soil treatment compared with the other soil texture–GWT depth combinations.

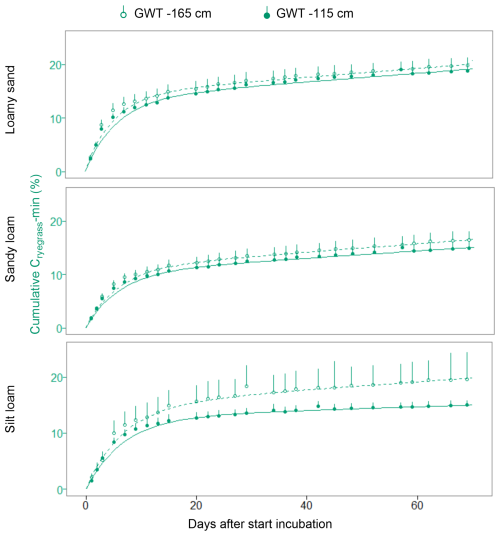
Figure 5 Cumulative C_ryegrass-min (%) and the fitted parallel two-rate first-order kinetic model for both GWT treatments in loamy sand, sandy loam and silt loam soil columns (n=4).

Table 3 Parameters of the parallel two-rate first-order kinetic model characterizing the cumulative C_ryegrass-min for both GWT treatments in loamy sand, sandy loam and silt loam soil columns.

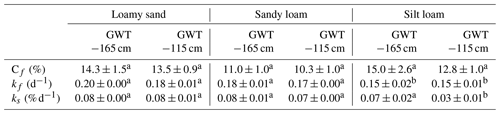
Letters indicate significant (P<0.1) differences between soil texture and GWT depth combinations for each parameter.

4 Discussion

With this experiment, we aimed to infer if and how the GWT depth (at either −165 or −115 cm) impacts topsoil moisture and C mineralization during simulated dry periods that could realistically occur in northwestern Europe. Below, we discuss the capillary moisture supply as a function of GWT–soil texture combinations (Sect. 4.1), the impact on OM mineralization (Sect. 4.2) and the consequences for modeling topsoil carbon at the landscape scale (Sect. 4.3).

4.1 To what extent does GWT depth affect moisture during simulated drought?

In the loamy sand columns, with a GWT of −165 cm, the moisture of the shallow layers (−30 and −10 cm) was consistently low (∼0.1 m³ m⁻³) and, thus, situated in the “dry” range of the soil water retention curve (Fig. B1 in Appendix B). There was clear evidence that the capillary moisture supply from deeper soil layers towards the topsoil was insignificant for this deepest GWT treatment. First, although positive hydraulic head differences (ΔH) between −60 and −30 cm enabled capillary action, these differences displayed an increasing trend throughout the experiment (Fig. 3). Hence, the soil was observed to be drying out at 105 and 135 cm above the GWT, clearly indicating that evaporative losses were insufficiently compensated for by a capillary water flux. Second, hydraulic head differences between −30 and −10 cm depth were even negative, excluding upward moisture transport out of the directly underlying subsoil. In fact, watering events likely caused temporary downward moisture fluxes between these topsoil layers, as indicated by the fluctuating pattern of ΔH (−30 to −10 cm). Considering the moisture retention curve, it emerges that stronger suction forces than those recorded here would also not have readily resulted in marked further soil drying, which explains why moisture at −30 cm remained relatively constant despite temporal changes in ΔH. In summary, the absence of a significant upward moisture supply to the loamy sand topsoil with a deep GWT is most likely directly attributable to an overly limited capillary rise height characteristic of this texture. When the GWT was raised to −115 cm, moisture at −30 cm was higher than at −165 cm GWT, implying that upward capillary moisture flow markedly impacted soil moisture up to at least 85 cm above the GWT, less so beyond 105 cm and not at all beyond 135 cm.

In the sandy loam and silt loam soil columns, the GWT depth did clearly affect the topsoil moisture, with higher water contents when the GWT was at −115 cm compared with at −165 cm. Hence, it seems likely that upward moisture flow in the sandy loam and silt loam columns by capillary action reached at least up to a height of 135 cm. For the silt loam soils, water contents were also consistently high (∼0.310 m³ m⁻³) up to 105 cm above the −165 cm GWT; thus, the capillary fringe likely extended beyond 135 cm above the GWT.

Our findings are substantiated by the calculated hydraulic head differences, especially with respect to the (dis)continuity in evaporation from the topsoil layer. For example, negative ΔH between −30 and −10 cm for the loamy sand during the −165 cm GWT treatment indicated that evaporation ceased, whereas this did not seem to be the case for the other soil texture–GWT combinations. However, ΔH was unexpectedly negative between −120 and −85 cm for the −165 cm GWT treatment of the loamy sand and sandy loam columns. These observations imply downward moisture transport, which could be the case if macropores served as preferential flow pathways. However, as we observed an increase in water content during the shallower GWT treatments above this soil segment, upward moisture movement would have been the dominant water flow, with the GWT as the starting point for the flow path. We believe that these unexpected negative ΔH values are, therefore, more likely a result of cumulative errors when converting measured θ_V into H using soil water retention curves obtained from drying phases. Due to hysteresis, such curves can be inaccurate for soil wetting (Hillel, 2003), which was the main expected process at the considered deeper depths near the GWT. In retrospect, a better experimental approach would have been to directly measure the hydraulic head using compact tensiometers, especially in the undisturbed parts of the soil columns, where following moisture transport was the main objective. However, even for the smallest laboratory-scale models, their installation would likely have caused significant disturbance to the soil columns, in contrast to the volumetric sensors used in this study, which had very sharp, fine rods that were able to pierce the waterproof foil surrounding the soil columns with minimal disruption.

In summary, our experiment revealed that upward moisture transport from the GWT to the topsoil occurs when the GWT depth is located within specific depth ranges depending on texture, with a larger impact on moisture supply at a shallower (closer to the topsoil) depth. For the loamy sand soils, the depth of the GWT that is still able to affect topsoil via capillary moisture supply was estimated to be 85 cm below the surface. For sandy loam, topsoil moisture supply occurred for GWT depths of up to 135 cm below the soil surface. Finally, for silt loam soils, it seemed that capillary moisture supply from the GWT at deeper depths than those tested here would still markedly affect the topsoil. Prior laboratory experiments have observed a capillary moisture supply from the GWT up to heights of 117 and 149 cm for loamy sand soils and up to 175 and 183 cm for sandy loam soils (Malik et al., 1989; Shaw and Smith, 1927). In another study (Lane and Washburn, 1947), upward moisture transport was seen up to 240 cm for soils with a D₁₀ (diameter that 10 % of the particles in the particle-size distribution curve are finer than) of 0.02 mm, which should resemble our silt loam soil (Mozaffari et al., 2022). These reported results are based on setups with repacked soil columns, which do not reflect the soil structure under in situ conditions. In contrast, our undisturbed soil columns included small-scale heterogeneities, with features such as macropores, small stones and cracks, as they would occur in the field (Lewis and Sjöstrom, 2010), and this probably explains the somewhat lower capillary rise heights found for loamy sand in our experiment. Moreover, our setup was located in a temperature-controlled dark room, where environmental conditions do not approach the field situation. Ambient outdoor wind, temperature and relative air humidity determine evaporation from the topsoil and, thus, also indirectly co-drive the upward suction force across the soil profile (Huo et al., 2020). Nevertheless, overall, we expect that soil texture, structure and GWT depth predominantly dictate the height of capillary rise. Consequently, as we worked with 2 m undisturbed soil columns and realistic GWT depths, we do expect findings of GWT-dependent capillary moisture supply and topsoil moisture to be representative of the field situation. Indeed, when the GWT is deeper than the so-called evaporation characteristic length, hydraulic pathways become disconnected, and even high evaporative demands will not lead to a notable topsoil moisture supply (Balugani et al., 2018; Shokri and Salvucci, 2011). This was also observed in the coarser-textured loamy sand soil in our study.

4.2 Impact of GWT on topsoil OM decomposition

Soil water content (θ_V or percentage WFPS) determines soil heterotrophic activity and OM mineralization via a bell-shaped relationship (Manzoni et al., 2012; Moyano et al., 2013; Skopp et al., 1990; Yan et al., 2018). Particularly in the moderately dry range, the response of OM mineralization to volumetric soil moisture is strong, whereas water potential is generally a better predictor at a lower water content. Given the occurring moisture range and to avoid the conversion of measured volumetric moisture through soil water retention (pF) curves sensitive to hysteresis, we further used the percentage WFPS as a more directly obtained measure of soil moisture. As average topsoil moisture was significantly higher in the −115 cm GWT compared with the −165 cm GWT treatment for the sandy loam (38 % compared with 31 % WFPS) and silt loam (43 % compared with 33 % WFPS) soils, we accordingly expected promotion of OM mineralization at a shallower GWT for these two soil textures. In loamy sand, a shallower GWT only slightly increased topsoil moisture (28 % vs. 25 % WFPS), and so a minimal effect on OM decomposition may be expected. Surprisingly, however, the GWT-treatment-induced moisture differences did not have the expected effect on C_ryegrass mineralization rates (Fig. 4). Moreover, the cumulative 70 d C_ryegrass-min proved to be lower for the shallower −115 cm GWT treatment (Fig. 5). However, these observations need to be interpreted with care, as the GWT-treatment-induced topsoil moisture differences only occurred after day 8, while mineralization rates were an order of magnitude greater during the first 5 d compared with values later on. Nevertheless, about one-half to two-thirds of the cumulative C_ryegrass-min occurred early in the first weeks of the experiment. This implies that the effect of the GWT treatment on C_ryegrass-min should not be evaluated based on the 70 d cumulative C_ryegrass-min; rather, it should be examined after several weeks, with the GWT-treatment-imposed topsoil moisture differences being effective by then. From the fitted kinetic model, it emerges that the easily mineralizable C_ryegrass pool had already been mineralized at around day 14 for the loamy sand and sandy loam soil and at day 20 for the silt loam soil. Thereafter, the cumulative C_ryegrass-min followed a relatively constant course (i.e., it was determined by the mineralization of a more stable C_ryegrass pool); therefore, the evaluation of the GWT impact on topsoil C_ryegrass mineralization should further solely be based on the effects on the mineralization rate of the more stable C_ryegrass pool (k_s). We accordingly expected lower k_s estimates with a deeper GWT. However, there was no effect of the GWT on k_s for the loamy sand or sandy loam soils, while it was even lower for the −115 cm GWT treatment for the silt loam soils than for the −165 cm GWT treatment (0.03 vs. 0.07 % d⁻¹, respectively). Thus, these results lead us to reject the hypothesis that a higher GWT-induced topsoil moisture availability would promote topsoil C mineralization.

To interpret these seemingly illogical effects, it is important to consider the complexity of the relationship between soil moisture and C mineralization, especially when moisture fluctuates as it did in our experiment. This is in contrast to typical experiments to infer the bell-shaped θ_V–C mineralization relationship in which moisture is held constant. Notably, it is well known that rewetting of dry soil triggers a pulse of microbial activity, resulting in a CO₂ flush – referred to as the Birch effect (Barnard et al., 2020; Birch, 1958). Former studies have found that these respiration pulses become larger with larger changes in the soil moisture state upon rewetting as well as with drier pre-wetting soil conditions (Fischer, 2009; Harrison-Kirk et al., 2013; Lado-Monserrat et al., 2014; Manzoni et al., 2020; Unger et al., 2010). For example, Harrison-Kirk et al. (2013) observed an increased Birch effect in silt loam soils when the pre-wetting moisture state was reduced from 33 % to 22 % WFPS. Indeed, particularly shortly after water applications later in our experiment, the rates tended to deviate between both GWT treatments, with a stronger temporary stimulation in the drier pre-wetting, −165 cm GWT (24 %, 27 % and 29 % WFPS) topsoil, when compared with the wetter, shallower, −115 cm GWT treatment (26 %, 35 % and 39 % WFPS for the loamy sand, sandy loam and silt loam soils, respectively) (Fig. 4). Accordingly, a potential explanation could be that the drier topsoil condition with a deeper GWT may have amplified the Birch effect, i.e., rewetting C mineralization pulses caused by the watering events. In the light of this, it is possible that the expected enhancement of C mineralization (as represented by k_s) due to increased moisture from capillary action under shallower GWT depths was offset in loamy sand and sandy loam soils and perhaps even overruled in silt loam soils by a stronger Birch effect in drier soils with a lower capillary moisture supply. In other words, the reduced mineralization rates observed in silt loam under a shallower GWT (k_s) might be explained, at least in part, by a larger capillary moisture supply compared with the other soil texture–GWT combinations, although other factors, such as an intertwined effects between moisture and temperature, could also be at play. As dry–wet cycles are expected to intensify with climate change in Europe, i.e., longer periods of drought followed by intense rainfall events (Toreti et al., 2022), such GWT-induced control on moisture variations and consequences for the C budget must be carefully considered.

4.3 Consequences for modeling moisture and SOC balances at the larger spatial landscape scale

Based on our findings, it emerges that variation in the GWT at relatively shallow depths, as seen in a large part of our study area (northwestern Europe), will contribute to spatial variation in topsoil moisture during periods of limited rainfall. Accordingly, Meles et al. (2020) adapted the commonly used topography wetness index by inversely weighting it with the GWT depth, resulting in a more accurate index for low-slope landscapes, such as our study region. Ukkola et al. (2016) further reported that there is a systematic tendency among numerous land surface models to overestimate the consequences of drought. They attributed this to the assumption of a free-draining soil boundary in these models; i.e., the GWT is not taken into account. According to our results, the hydrological modules that calculate water fluxes between adjacent layers, although with free-draining lower boundaries, applied in some soil C models, e.g., DayCent (Schimel et al., 2001), would be less accurate for the simulation of topsoil moisture during periods with limited rainfall, as these models do not incorporate capillary moisture flow when simulating recharge and presuppose that water draining from the soil profile is lost. The discrepancy with real physical processes occurring in the soil becomes even larger for models that employ a simplistic cascade bucket approach, such as DSSAT (Jones et al., 2003), Biome-BGC (Thornton and Law, 2010), CERES (Gabrielle et al., 1995) and CANDY (Franko et al., 1995). Only a limited number of biogeochemical models calculating water fluxes also include bidirectional water flow between the saturated and unsaturated zones by defining or even calculating a dynamic GWT, e.g., LandscapeDNDC (Haas et al., 2013; Liebermann et al., 2018) and DAISY (Abrahamsen and Hansen, 2000). However, a question remains regarding how accurately such models can simulate upward moisture supply and relate C mineralization to water content, particularly under dry conditions. With respect to this question, Moyano et al. (2013) concluded that the predictive capacity of current models is still questionable and that these models should incorporate physically based transport mechanisms for solutes, coupled with a more detailed portrayal of biological reactions to alterations in soil moisture. In order to reproduce respiration patterns caused by phenomena like the Birch effect, Evans et al. (2016) accordingly argued that models should include physicochemical mechanisms linking the water content to microbial growth and to diffusion.

Although the two GWTs in our 70 d experiment did not suggest a severe impact of the GWT on C mineralization, we should not generally conclude that the capillary moisture supply is an irrelevant process in soil C models. When meteorological droughts extend over periods longer than that simulated here, the combination of a limited moisture supply and increased evaporation might not only lead to soil moisture deficits but should also diminish groundwater recharge over the longer term (Brauns et al., 2020). This process could then lead to a further reduction in the topsoil water content, creating a positive feedback system. As a result, the GWT could, in turn, deepen further than usually anticipated during summer, which has in fact been observed over the past few years in areas such as Flanders, Belgium (VMM, 2022). Especially for croplands in northwestern Europe with a GWT close to the evaporation characteristic length, a tipping point in their moisture balance may be reached under future expected prolonged periods of drought in spring or summer. We conclude that soil models that are able to simulate upward moisture supply through capillary action and phenomena such as the Birch effect are better positioned to anticipate soil C trends.

5 Conclusion

Variation in the GWT depth, as is typical for arable land in northwestern Europe, was found to significantly impact the soil moisture profile of finer-textured soils during periods with limited rainfall. Here, the expected texture-dependent reach of soil moistening by capillary rise could be quantified as 85 cm above the GWT for loamy sand soils and 135 cm for sandy loam and silt loam soils. For situations in which the GWT is within these ranges, our findings should motivate the inclusion of bidirectional water flow, i.e., drainage and capillary transport, in soil models. Nevertheless, contrary to our hypothesis, a rise in the GWT did not enhance the decomposition of the added substrate (ryegrass). Moreover, we found that, after rewetting, C mineralization pulses were larger for the deepest GWT treatment. We hypothesize that, as soil was drier for the deeper GWT owing to less capillary moisture supply, the imposed rewetting events caused stronger Birch effects. Hence, not just the topsoil moisture state itself but also the extent of its fluctuation over time probably culminate in the overall net effect of the GWT depth on the C mineralization observed here. To employ empirical data from experiments like this to improve soil models, further studies will be needed to deconvolute the effects of soil moisture regimes on soil C mineralization. During prolonged periodic droughts, which are expected to become more frequent in future, correct simulation of the mostly neglected capillary moisture transport may become imperative for reliable simulation of C cycling in agricultural land in northwestern Europe.

Appendix A

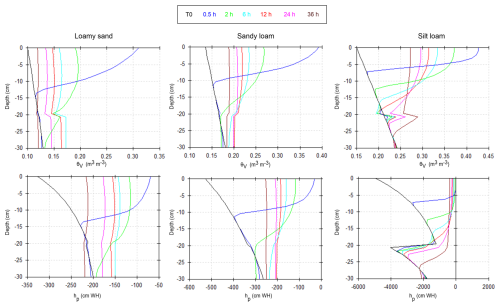
Figure A1 Simulations using HYDRUS-1D to determine when the water, added at an initial time point (T₀), reached the lower boundary of the repacked topsoil containing ¹³C-labeled ryegrass (at −20 cm depth). A 24 h period after water addition was found to be sufficient for all three soil textures (loamy sand, sandy loam and silt loam) to reach an approximately constant moisture level across the topsoil layer.

Figure A2 Sensors installed at a depth of −10 cm in sandy loam columns 1, 3 and 4 during the −115 cm GWT treatment were subjected to a correction via linear regression.

Table A1 Comparison of the volumetric water content measured with sensors at −10 cm and at the start and the end of the incubation of each groundwater treatment (“Validation”). Sensor values indicated with “^∗” were subjected to a correction via linear regression (see Fig. A2).

Appendix B

Figure B1 Soil water retention (pF) curves for different depths in our soil columns (n=4; except at −10 cm, where n=2).